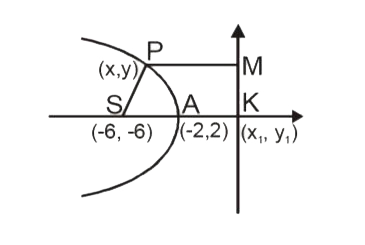
Find the equation of the parabola whose focus is (–6, –6) and vertex (–2, 2).
Let S(–6, –6) be the focus and A(–2, 2) is vertex of the parabola. On SA take a point K(x1,y1) such that SA = AK. Draw KM perpendicular on SK. Then KM is the directrix of the parabola.
Since A bisects SK,
(−6+x12,−6+y12)=(−2,2)
!−6+x1=−4
and −6+y1=4
or (x1,y1)=(2,10)
Hence the equation of the directrix KM is
y – 10 = m(x + 2)
Also gradient of SK
=10−(−6)2−(−6)
=168=2
!m=−12
y−10=−12(x−2) (from (i))
!x+2y–22
= 0 is the directrix
Next, let PM be a perpendicular on the directrix KM from any point P(x, y) on the parabola. From SP = PM, the equation of the parabola is
√{(x+6)2+(y+6)2}
=|x−2y−22|√(12+22)
or 5(x2+y2+12x+12y+72)=(x+2y–22)2
or 4x2+y2–4xy+104x+148y–124=0
or (2x–y)2+104x+148y–124=0.
Related Playlists
- BOOK - MOTIONCHAPTER - PARABOLAEXERCISE - EXERCISE - I28videos
PARABOLA
- BOOK - MOTIONCHAPTER - PARABOLAEXERCISE - EXERCISE - II17videos
PARABOLA
- BOOK - MOTIONCHAPTER - MONOTONOCITYEXERCISE - Exercise - 4 ( Level-II ) Previous Year (Paragraph)2videos
MONOTONOCITY
- BOOK - MOTIONCHAPTER - PERMUTATION AND COMBINATION EXERCISE - EXAMPLE23videos
PERMUTATION AND COMBINATION
Similar Questions
Find the equation of the parabola whose focus is (3,0) and vertex is (0,0).
View SolutionFind the equation of the parabola whose focus is (4,-3) and vertex is (4,-1).
View SolutionFind the equation of the parabola whose focus is at (0, 0) and vertex is at the intersection of the line x+y=1andx−y=3.
View Solutionfind the equation of parabola whose focus is (5,2) and vertex is at (3,2)
View SolutionFind the equation of the parabola whose focus is (1,−1) and whose vertex is (2,1). Also find the axis and latusrectum.
View SolutionFind the equation of the parabola whose focus is (6, 0) and directrix is x=−6.
View SolutionFind the equation of the parabola whose focus is (2, 3) and directrix is x−2y−6=0.
View SolutionFind the equation of the parabola whose focus is (−1,2)anddirectrixisx-2y-15=0.
View SolutionFind the equation of the parabola, if the focus is at (−6,−6) and the vertex is at (−2,2)
View SolutionFind the equation of the parabola whose focus is (2, 0) and directrix is x=−2.
View Solution


