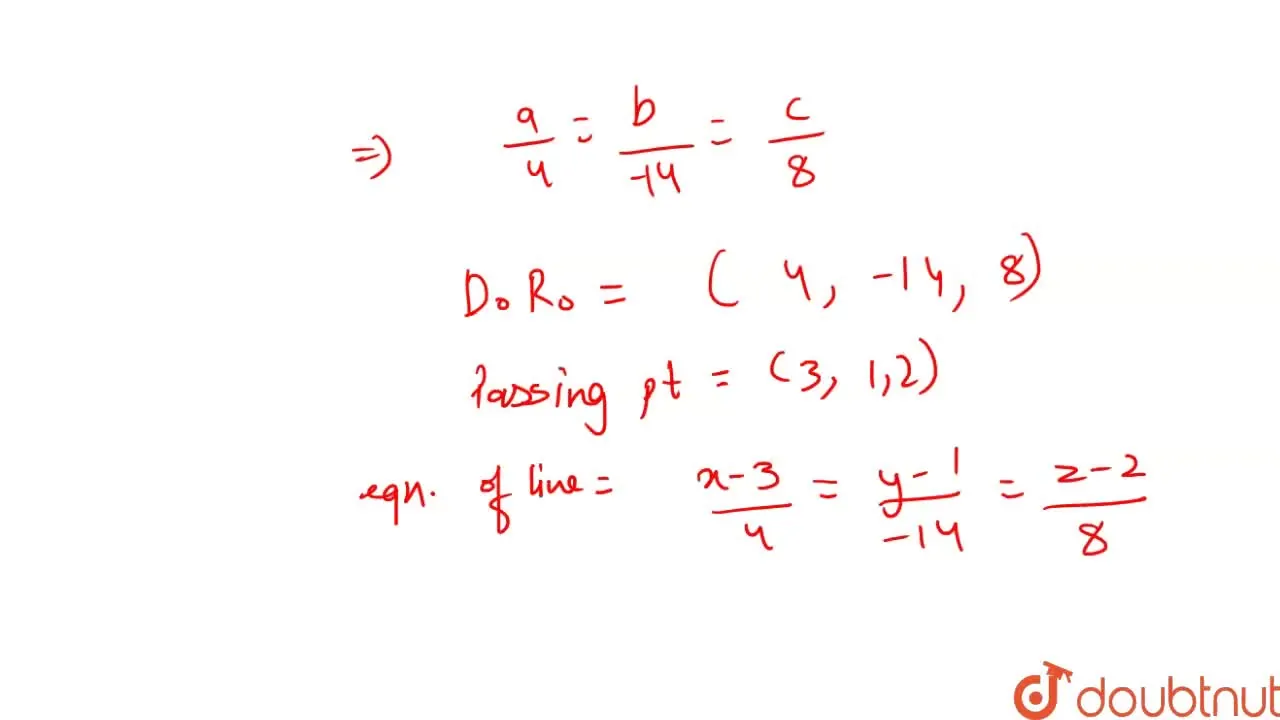Find the equation of the line passing through the point ( 3, 1, 2) and perpendicualr to the lines x−11=y−22=z−33andx−3=y2=z5.
Let a, b , c be the direction ratios of the required ratios of the required line which is perpendicular to the lines
x−11=y−22=z−33andx−3=y2=z5.
∴ a+2b+3c = 0 and -3a + 2b + 5c = 0
= a∣∣∣2325∣∣∣=−b∣∣∣13−32∣∣∣=c∣∣∣12−32∣∣∣
∴a10−6=−b(5+9)=c2+6
∴a4=b−14=c8
∴ the direction ratios of the requored line are 4, - 14 n , 8 i.e., 2, -7, 4.
The equation of the line passing through the point (x1,y1,z1) and having the directions ratios a, b ,c is x−x1a=y−y1b=z−z1c
∴ the equation of the required line passing through A(3,1,2) and having directions ratios 2, - 7 , 4 is
x−32=y−1−7=z−24.
Related Playlists
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINEEXERCISE - Theory1videos
LINE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINEEXERCISE - examples for practice20videos
LINE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - INTEGRATIONEXERCISE - Multiple Choice Questions15videos
INTEGRATION
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINEAR PROGRAMMING EXERCISE - EXAMPLES FOR PRACTICE8videos
LINEAR PROGRAMMING
Similar Questions
(i) Find the vector and cartesian equation of the line passing through the point (1,2,-4) and perpendicular to the two lines :
x−83=y+19−16=z−107andx−153=y−198=z−5−5 .
(ii) Find the vector and cartesian equations of the line passing through the point (2,1,3) and perpendicular to the lines :
x−11=y−22=z−33andx−3=y2=z5 .View SolutionFind the equation of the line passing throught the point (2,1,3) and perpendicular to the lines x−11=y−22=z−33 and x−3=y2=z5.
View SolutionFind the equation of the line passing through the point (3,1,2) and perpendicular to the lines x−11=y−22=z−33 and x−3=y2=z5
View SolutionFind the equation of the line passing through the point (2, 1, 3) and perpendicular to the lines x−11=y−22=z−33andx−3=y2=z5
View SolutionFind the equations of the line passing through the point (-1,3,-2) and perpendicular to each of the lines x1=y2=z3 and x+2−3=y−12=z+15
View SolutionWhat is the equation of the line passing through the point (1,2,3) and perpendicular to the lines x+11=y+22=z+33 and x−3=y2=z5 ?
View SolutionFind the vector equation of the line passing through the point (1,−1,2) and perpendicular to the plane 2x−y+3z−5=0.
View Solution(i) Find the equations of the straight line passing through the point (2,3,-1) and is perpendicular to the lines :
x−22=y+11=z−3−3andx−31=y+21=z−11 .
(ii) Find the equation of the line which intersects the lines :
x+21=y−32=z+14andx−12=y−23=z−34
Perpendicular and passes through the point (1,1,1) .View SolutionFind the equation of the line passing through the point (1, 2, 3) and perpendicular to the lines
x−13=y−31=z−4−5andx−11=y−22=z−33View SolutionFind the equation of the line passing through the point (−1,2,3) and perpendicular to the lines x2=y−1−3=z+2−2andx+3−1=y+32=z−13.
View Solution