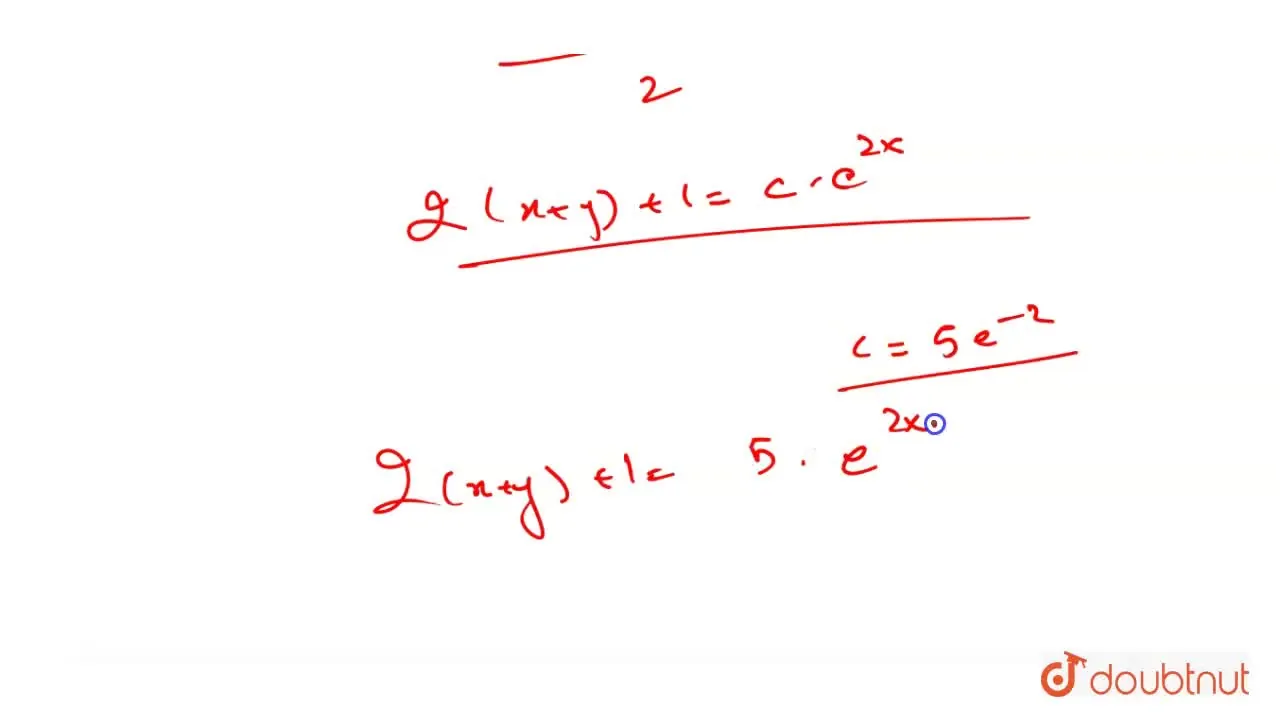Find the equation of the curve passing through (1, 1) and the slope of the tangent to curve at a point (x, y) is equal to the twice the sum of the abscissa and the ordinate.
∵ The slope of the tangent at (x, y) is dydx
∴dydx=2(x+y) ...(1)
Let x + y = t
⇒1+dydx=dtdx
∴ From equation (1)
dtdx−1=2t
⇒dt2t+1=dx
Integrating both sides, we get
12ln(2t+1)=x+lnc1
⇒ln(2t+1)=2x+lnc, where lnc=2lnc1
⇒2t+1=ce2x
or 2(x+y)+1=ce2x
∵ The curve passes through (1, 1)
∴2(1+1)+1=ce2
⇒c=5e−2
∴ The equation of the curve is 2(x+y)+1=5e2(x−1)
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Try Yourself26videos
DIFFERENTIAL EQUATIONS
- BOOK - AAKASH INSTITUTECHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Assignment (Section - A) Competition Level Questions35videos
DIFFERENTIAL EQUATIONS
- BOOK - AAKASH INSTITUTECHAPTER - DETERMINANTS EXERCISE - SECTION - J12videos
DETERMINANTS
- BOOK - AAKASH INSTITUTECHAPTER - INTEGRALSEXERCISE - Try yourself50videos
INTEGRALS
Similar Questions
Find the equation of a curve passing through (1,1) and whose slope of tangent at a point (x, y) is −xy.
View SolutionFind the equation of the curve passing through origin if the slope of the tangent to the curve at any point (x,y)is equal to the square of the difference of the abscissa and ordinate of the point.
View SolutionFind the equation of a curve passing through the point (0, 1). If the slope of the tangent to the curve at any point (x, y) is equal to the sum of the x coordinate (abscissa) and the product of the x coordinate and y coordinate (ordinate) of that point.
View SolutionFind the equation of a curve passing through the origin given that the slope of the tangent to the curve at any point (x, y) is equal to the sum of the coordinates of the point.
View SolutionFind the equation of the curve passing through the point (0,0) and whose slope of the normal at a point (x, y) is equal to the sum of the ordinate and the product of the abscissa and ordinate of that point.
View SolutionFind the equation of the curve which passes through (1,0) and the slope of whose tangent at (x,y) is x2+y22xy
View SolutionFind the equation of the curve passing through the point (1,0) if the slope of the tangent to the curve at any point (x,y)isy−1x2+x.
View SolutionFind the equation of a curve, passes through (−2,3) at which the slope of tangent at any point (x,y) is 2xy2.
View SolutionFind the equation of the curve through the point (1,0), if the slope of the tangent to the curve at any point (x,y) is y−1x2+x
View SolutionDetermine the equation of the curve passing through the origin , the slope of the tangent of which at any point(x,y) is x+1y+1 .
View Solution