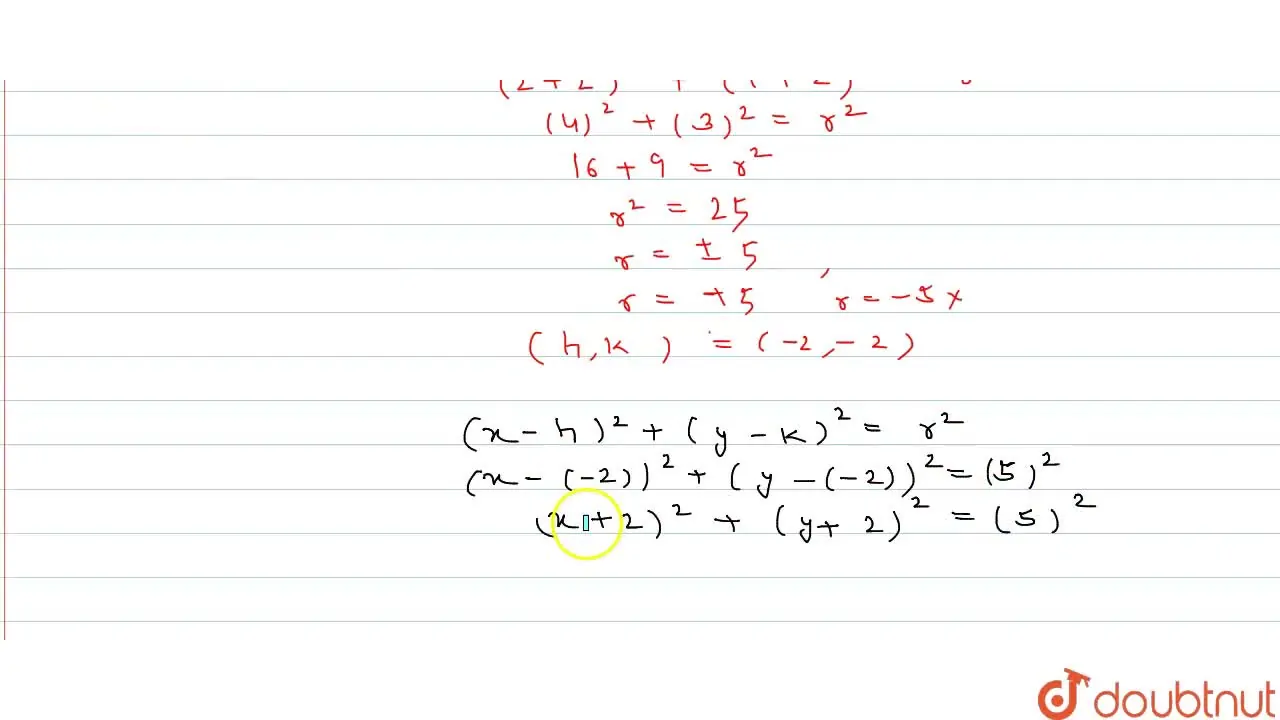Find the equation of the circle passes through the points (2,1) and (−2,3) and has centre on the line x+y+4=0
Let the equation of the circle be (x−h)2+(y−k)2=r2
Since the circle passes through (2,1) and (−2,3)
We have, (2−h)2+(1−k)2=r2 …(1)
and (−2−h)2+(3−k)2=r2 ...(2)
SInce the centre lies on the line x+y+4=0
∴ Wehave,h + k + 4 =0...(3)
Equation (1) and (2) we get :
(2−h)2+(1−k)2=(−2−h)2+(3−k)2
⇒2h−k+2=0
Solving (4) and (3), we get
h=−2 and k=−2
Now, putting the values of h and k in (1), we get,
[2−(2)]2+[1−(−2)]2=r2
⇒16+9=r2
⇒r=±5
The value of r cannot be negative,
∴r=5,(h,k)=(−2,−2)
Hence, equation of the required circle is [x−(−2)]2+[y−(−2)]2=(5)2
i.e., (x+2)2+(y+2)2=(5)2
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - CONIC SECTIONSEXERCISE - Try ypurself42videos
CONIC SECTIONS
- BOOK - AAKASH INSTITUTECHAPTER - CONIC SECTIONSEXERCISE - Assignment (SECTION - A)55videos
CONIC SECTIONS
- BOOK - AAKASH INSTITUTECHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - section-J (Aakash Challengers Qestions)16videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
- BOOK - AAKASH INSTITUTECHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - section - J6videos
CONTINUITY AND DIFFERENTIABILITY
Similar Questions
Find the equation of the circle passing through the points (0,−1)and(2,0) and whose centre lies on the line 3x+y=5
View SolutionFind the equation of the circle passing through the points (4, 1) and (6, 5) and whose centre is on the line 4x+y=16.
View SolutionFind the equation of the circle which passes through the points (3, -2), (−2,0) and has its centre on the line 2x−y=3.
View SolutionFind the equation of the circle which passes through the points (1,3)and(2,−1), and has its centre on the line 2x+y−4=0
View SolutionFind the equation of the circle which passes through the points (−1,2)and(3,−2) and whose centre lies on the line x−2y=0.
View SolutionFind the equation of the circle passing through the points (2,3)and (−1,1)and whose centre is on the line x−3y−11=0.
View SolutionWhat is the equation of the circle which passes through the points (3 , -2) and (-2,0) and having its centre on the line 2x + y - 3 =0 ?
View SolutionFind the equaiton of the circle passing through the points (2,−3)and(3,−2) and whose centre lies on the line 2x−3y=8.
View SolutionFind the equation of the circle which passes through the points (3,7), (5,5) and has its centre on the line x−4y=1.
View SolutionFind the equation of the circle which passes through the points (3,−2)and(−2,0) and the center lies on the line 2x−y=3
View Solution