Find the equation of the circle having radius 5 and which touches line 3x+4y−11=0 at point (1, 2).
As shown in the figure, the two circles touch the line 3x+4y−11=0 at point (P(1,2).
∴ Centre lies on the line perpendicular to the tangent at P at distance 5 from it on either side.
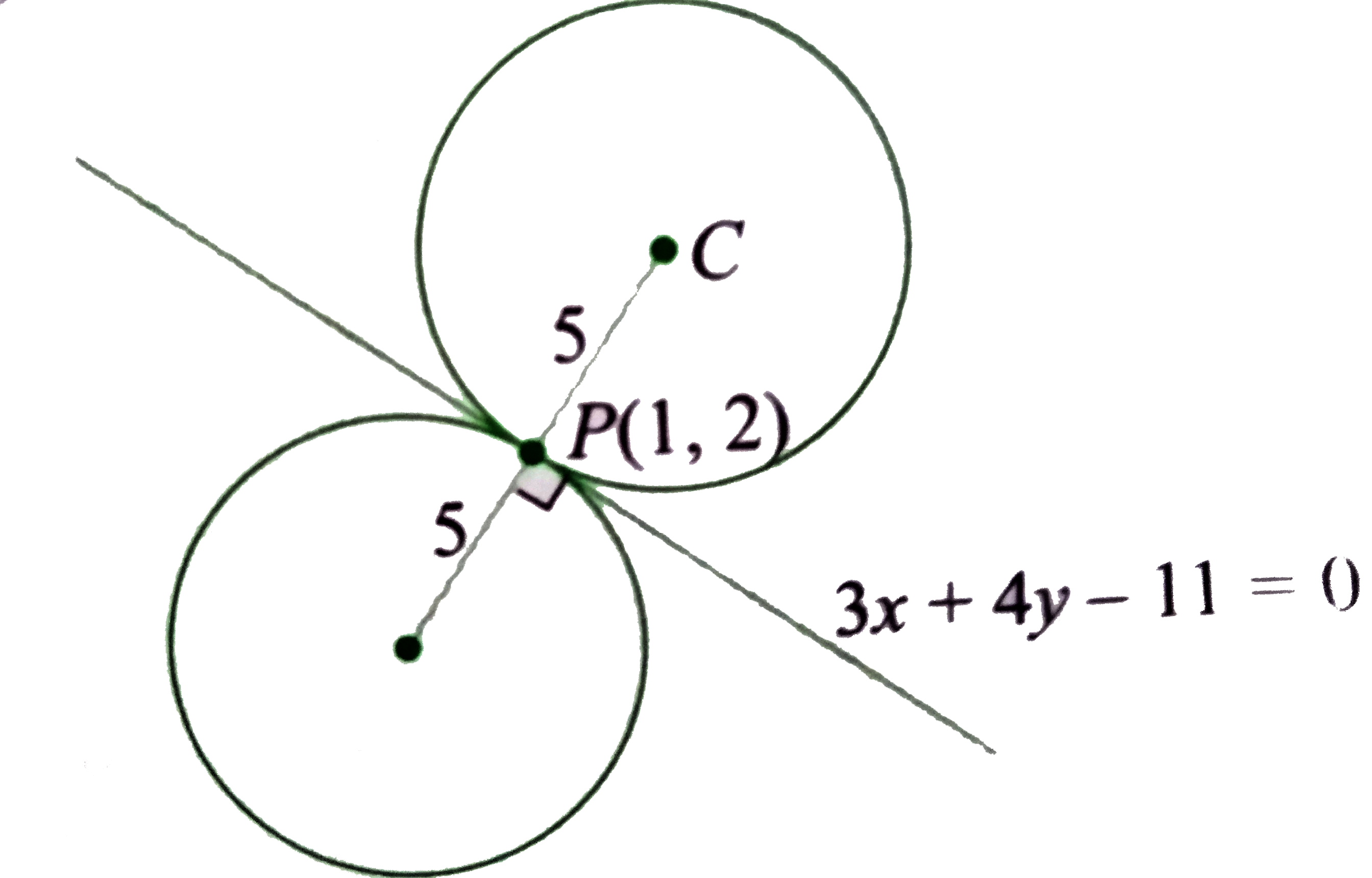
Slope of given tangent line is −34
Thus, the slope of CP is 43.
∴tanθ=43
∴Centre, C≡(1±5cosθ,2±5sinθ)
∴C≡(1±535,2±545)
∴C≡(4,6) or (−2,−2)
Therefore, equations of circles are
(x−4)2+(y−6)2=25
or (x+2)2+(y+2)2=25
Topper's Solved these Questions
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:Examples
Explore 13 Videos
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:CONCEPT APPLICATION EXERCISE 4.1
Explore 1 Video
- BINOMIAL THEOREMBook:CENGAGE ENGLISHChapter:BINOMIAL THEOREMExercise:Matrix
Explore 4 Videos
- CIRCLESBook:CENGAGE ENGLISHChapter:CIRCLESExercise:Comprehension Type
Explore 8 Videos
Similar Questions
Find the equation of the circle having center at (2,3) and which touches x+y=1.
View SolutionWrite the equation of the circle having radius 5. and tangent as the line' 3x - 4y +5 = 0 at (1,2).
View SolutionWrite the equation of the circle having radius 5 and tangent as the line 3x−4y+5=0 at (1,2)
View SolutionFrom a point P, tangents drawn to the circle x2+y2+x−3=0,3x2+3y2−5x+3y=0and4x2+4y2+8x+7y+9=0 are of equal lengths. Find the equation of the circle through P, which touches the line x+y=5 at the point (6,−1).
View SolutionFind the equation of the circle having centre at (3,−4) and touching the line 5x+12y−12=0.
View SolutionFind the equation of the circle having centre at (3,−4) and touching the line 5x+12y−12=0.
View SolutionFind the equation of the circle which has radius 5 units and which is tangent to the line 3x+4y−16=0 at the point (4, 1).
View SolutionFind the equation of the circle whose radius is 5 and which touches the circle x2+y2−2x−4y−20=0 externally at the point (5,5).
View SolutionFind the equation of the circle whose radius is 5 and which touches the circle x2+y2−2x−4y−20=0 externally at the point (5,5).
View SolutionFind the equation of the circle whose radius is 5and which touches the circle x2+y2−2x−4y−20=0 externally at the point (5,5).
View Solution

