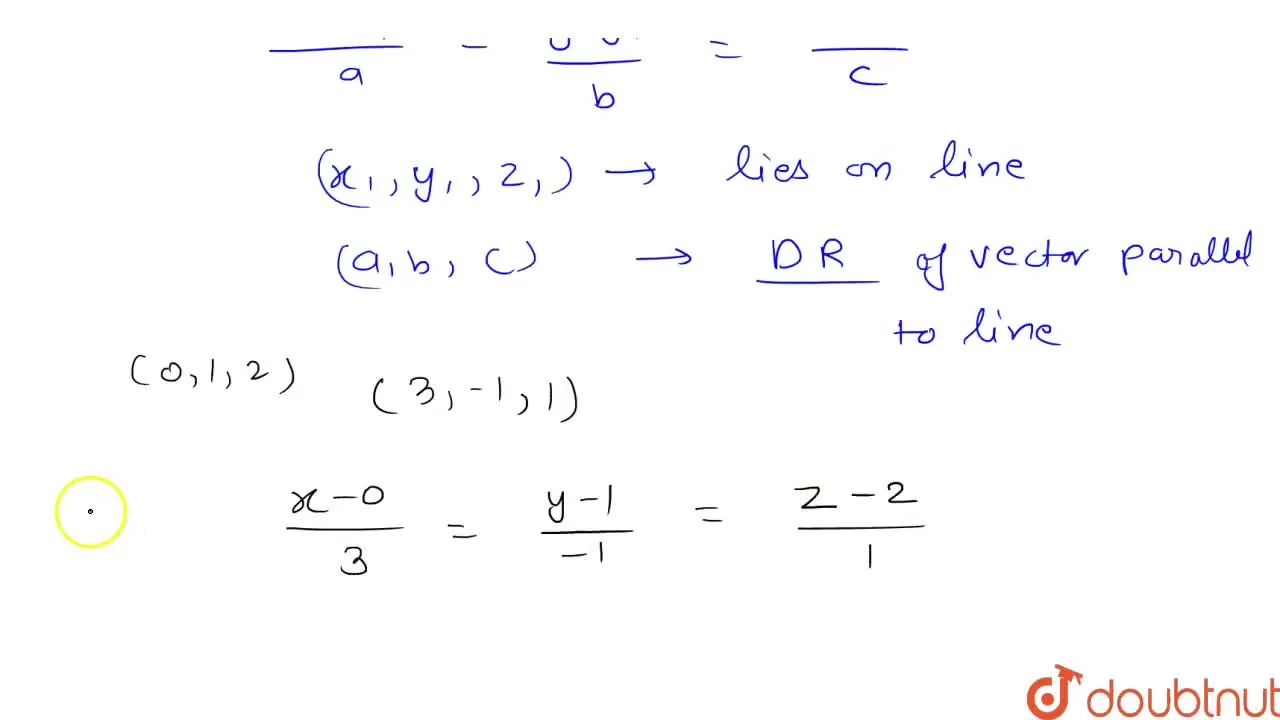Find the equation of line in Cartesian form passing Through (0, 1, 2) and is parallel to a vector
which have direction ratios (3, -1, 1) ?
We know that equation of line in Cartesian form which passes through (x1,y1,z1) and is parallel
to vector having direction ratios (a, b, c) is given by
x−x1a=y−y1b=z−z1c
Here (x1,y1,z1)≡(0,1,2)
(a,b,c)≡(3,−1,1)
so equation will be
x−03=y−1−1=z−21
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - Illustration4videos
THREE DIMENSIONAL GEOMETRY
- BOOK - AAKASH INSTITUTECHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - TRY YOURSELF97videos
THREE DIMENSIONAL GEOMETRY
- BOOK - AAKASH INSTITUTECHAPTER - STRAIGHT LINESEXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)5videos
STRAIGHT LINES
- BOOK - AAKASH INSTITUTECHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section - J (Akash Challengers Question)15videos
TRIGNOMETRIC FUNCTIONS
Similar Questions
Find the equation of line which passes through a point (-1, 2, 3) and is parallel to a vector
having direction ratios (3, 4, 2).View SolutionFind the equation of a line passing through the point (0,1) and parallel to :
3x−2y+5=0View SolutionEquation of plane passing through (1,0,1),(3,1,2) and parallel to the vector i−j+2k is
View SolutionFind the equation of the line in vector form passing through the points (2, -1, 3) and (3, 1, 2)
View SolutionFind the equation of the plane passing through the points (2,2,−1)and(3,4,2) and parallel to the line whose direction ratios are (7,0,6)
View SolutionFind the equation of the line in vector form passing through the points (1, 1, 0) and (-3, -2, -7).
View SolutionFind the vector equation of a plane passing through the point (1,2,3) and parallel to the lines whose direction ratos are (1,−1,−2) and (−1,0,2).
View SolutionFind the Cartesian equations of the line passing through (−1,−1,2) and parallel to the line 2x-2=3y+1=6z-2
View SolutionFind the vector equation for the line passing through the points (1,0,2)and (3,4,6).
View SolutionFind the vector equation of tha plane which passes through the point (3, 2, -3) and perpendicular
to a line with direction ratios (1, 2, -1).View Solution