Find the equation of a circle which passes through the origin and cuts off intercepts from the x - axis and the y - axis respectively.
Let the required equation of the circle be
… (i)
Clearly, the circle passes through the point
Putting in (i), we get c = 0
Thus (i) becomes
Putting in (ii) we get
.
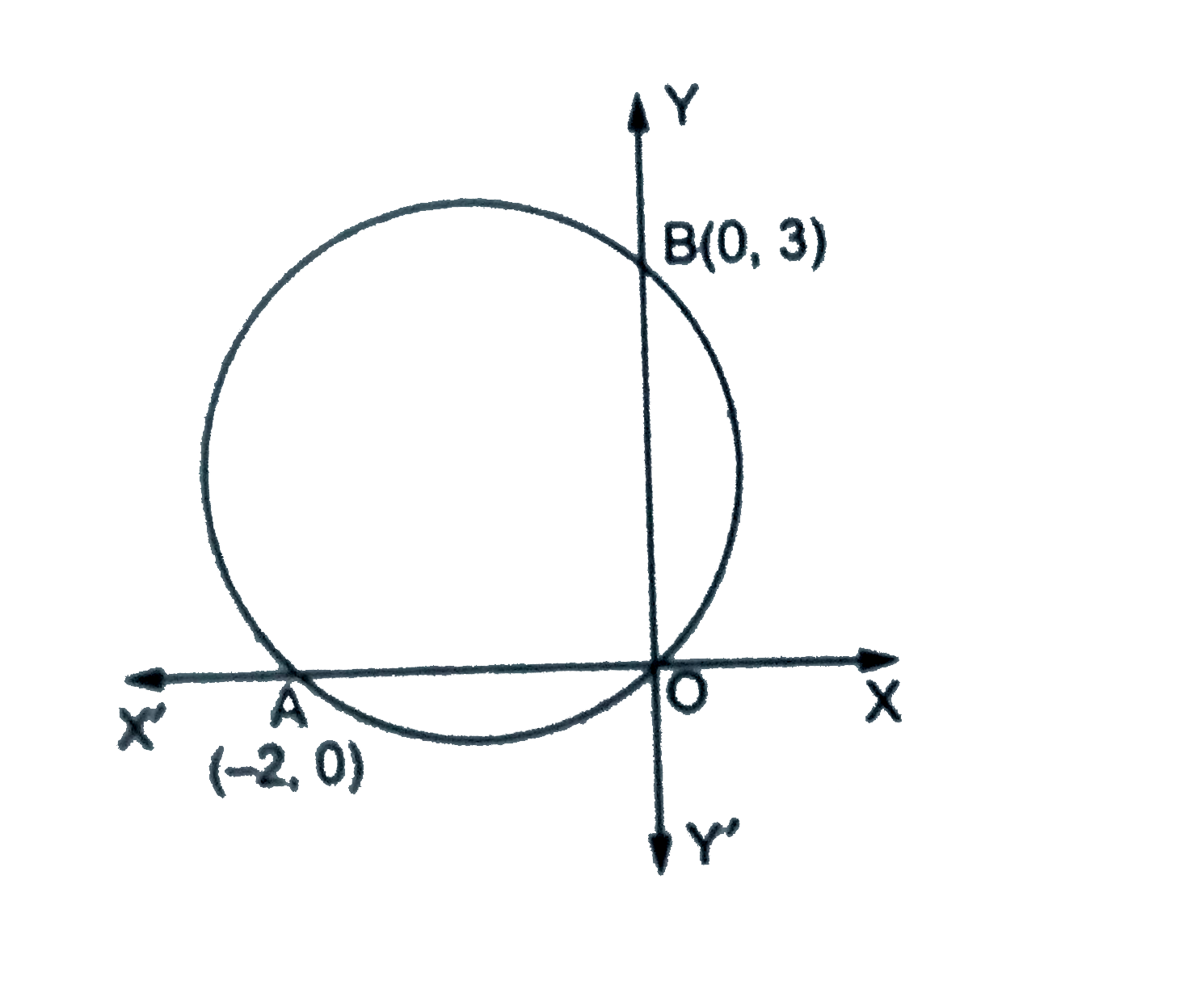
Putting in (iii), we get
Putting in (ii), we get
which is the required equation of the circle.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLE EXERCISE - EXERCISE 21 A14videos
CIRCLE
- BOOK - RS AGGARWALCHAPTER - CIRCLE EXERCISE - EXERCISE 21 B18videos
CIRCLE
- BOOK - RS AGGARWALCHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE 10B16videos
BINOMIAL THEOREM
- BOOK - RS AGGARWALCHAPTER - COMBINATIONSEXERCISE - Exercise 9D18videos
COMBINATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
The equation of circle which passes through the origin and cuts off intercepts 5 and 6 from the positive parts of the x-axis and y-axis respectively is (x−52)2=(y−3)2=λ, where λ is
A614B46C14D0 - Question 2 - Select One
If the equation of circle which passes through the origin and cuts off intercepts 5 and 6 from the positive parts of the X-axis and Y-axis respectively, is (x−52)2+(y−3)2=λ ,then λ equal is
A614B46C14D0 - Question 3 - Select One
The equation of the circle which passes through the origin and cuts off intercepts 3 and 4 from the positive of the axes, respectively is
A4x2+12xy+4y2−16y=0Bx2+y2−3x−4y=0C4x2−12xy+4y2+16y=0DNone of the above
Find the equation of the circle which passes through the origin and cuts off intercepts a and b respectively from x and y−axes.
View SolutionFind the equation of the circle which passes through the origin and cuts off intercepts 3and4 from the positive parts of the axes respectively.
View SolutionFind the equation of the circle, passing through the origin and cutting off intercepts 2a units and b units on the x-axis and y-axis respectively.
View Solution(i) Find the equation of a circle passes through the origin and cuts the intercepts of 6 units and 8 units on X-axis and Y-axis respectively.
(ii) Find the equation of a circle which passes through the two points on y-aixs whose distance from origin is 4 units and radius is 5 units.View SolutionFind the equation of the circle which passes through the origin and cuts of intercepts 3 units and 4 units from the positive parts of the x-axis and y-axis respectively.
View Solution
