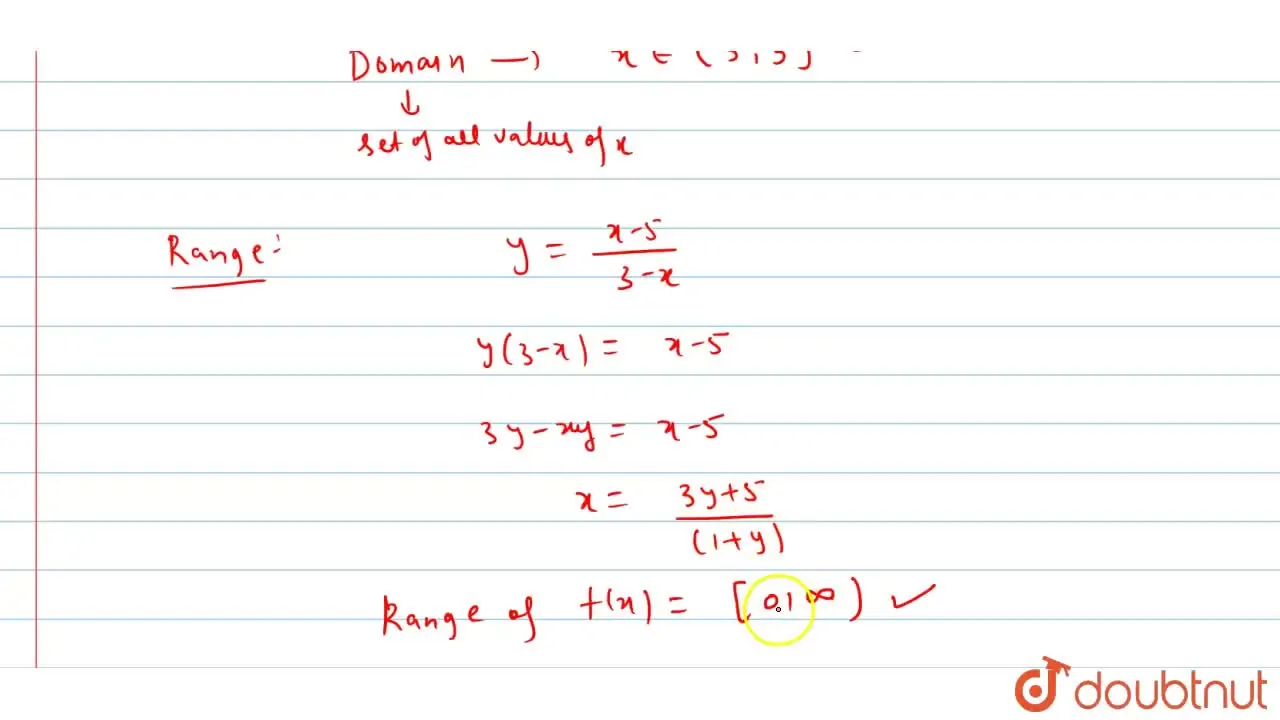Find the domain of the range of each of the following real functions:
The correct Answer is:dom
is defined only when .
Now, .
And,
Thus, f(x) is defined when .
.
Clearly, .
Let y=f(x). Then,
It followes from (i) that x is defined for each real value of y.
.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - FUNCTIONSEXERCISE - EXERCISE 3D4videos
FUNCTIONS
- BOOK - RS AGGARWALCHAPTER - FUNCTIONSEXERCISE - EXERCISE 3E5videos
FUNCTIONS
- BOOK - RS AGGARWALCHAPTER - FUNCTIONSEXERCISE - EXERCISE 3B8videos
FUNCTIONS
- BOOK - RS AGGARWALCHAPTER - ELLIPSEEXERCISE - EXERCISE26videos
ELLIPSE
- BOOK - RS AGGARWALCHAPTER - GEOMETRICAL PROGRESSIONEXERCISE - EXERCISE 12H (Very Short Answer Type Questions)13videos
GEOMETRICAL PROGRESSION
Similar Questions
Find the domain of the range of each of the following real functions:
f(x)=√3x−5View SolutionFind the domain of the range of each of the following real functions:
f(x)=1x−5View SolutionFind the domain of the range of each of the following real functions:
f(x)=1xView SolutionFind the domain of the range of each of the following real functions:
f(x)=1√2x−3View SolutionFind the domain of the range of each of the following real functions:
f(x)=x−32−xView SolutionFind the domain of the range of each of the following real functions:
f(x)=x2−9x−3View SolutionFind the domain of the range of each of the following real functions:
f(x)=3x−2x+2View SolutionFind the domain of the range of each of the following real functions:
f(x)=|x−4|x−4View SolutionFind the domain of the range of each of the following real functions:
f(x)=1−|x−2|View SolutionFind the domain of the range of each of the following real functions:
f(x)=x2−16x−4View Solution