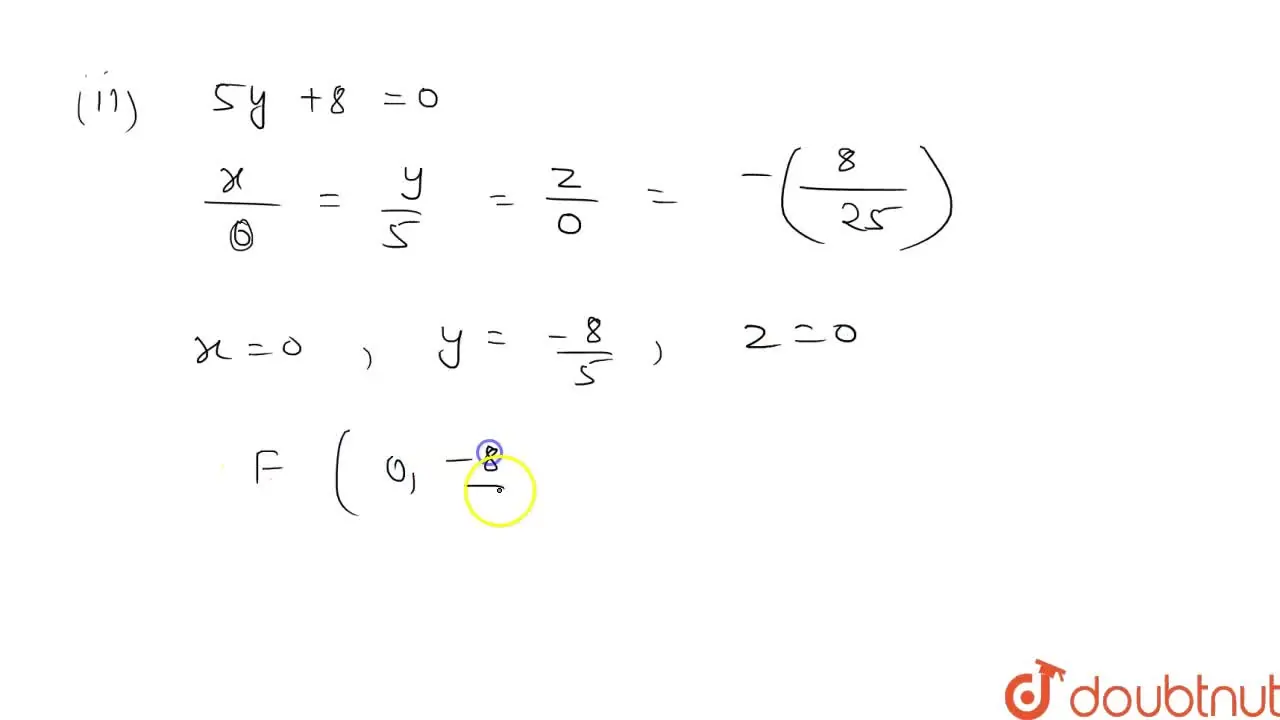Find the coordinates of the foot of the perpendicular drawn from the origin to the plane i) 2x+3y+4z−12=0, ii) 5y+8=0.
The correct Answer is:i) (2429,3629,4829), ii) (0,−85,0)
Given, equation is 2x+3y+4z=12…………..(i)
D.r.'s of normal to the plane are 2,3,4.
Equation of the line through O(0,0,0) and perpendicular to plane (i) is
x2=y3=z4=λ (say).
A general point on (ii), is N(2λ,3λ,4λ).
If this point lies on plane (i), then
(2×2λ)+(3×3λ)+(4×4λ)=12⇒29N=12⇒λ=1229.
Hence,the required point is (2429,3629,4829).
ii) The given plane is 0x−5y+0z=8..................(i)
D.r.'s of normal to the plane are 0,-5,0.
Equation of the line through O(0,0,0) and perpendicular to plane (i) are
x0=y−5=z0=λ (say)..............(ii)
A general point on this line (i), we have
−5×(−5λ)=8⇒25λ=8⇒λ=825.
Hence, the required point is N(0,−85,0).
Related Playlists
- BOOK - RS AGGARWALCHAPTER - THE PLANEEXERCISE - Exercise 28C34videos
THE PLANE
- BOOK - RS AGGARWALCHAPTER - THE PLANEEXERCISE - Exercise 28F18videos
THE PLANE
- BOOK - RS AGGARWALCHAPTER - THE PLANEEXERCISE - Exercise 28A9videos
THE PLANE
- BOOK - RS AGGARWALCHAPTER - SYSTEM OF LINEAR EQUATIONSEXERCISE - Objective Questions53videos
SYSTEM OF LINEAR EQUATIONS
- BOOK - RS AGGARWALCHAPTER - VECTOR AND THEIR PROPERTIESEXERCISE - Exercise 2224videos
VECTOR AND THEIR PROPERTIES
Similar Questions
Find the coordinates of the foot of the perpendicular drawn from the origin to the plane 2x−3y+4z−6=0.
View SolutionFind the coordinates of the foot of the perpendicular drawn from the origin to the plane 2x−3y+4z−6=0.
View SolutionFind the coordinates of the foot of the perpendicular drawn from the origin to the plane 3y+4z−6=0.
View SolutionFind the co-ordinate of the foot of the perpendicular drawn form the origin to the plane 5y+8=0
View SolutionThe coordinates of the foot of the perpendicular drawn from the origin to the plane 2x−3y+4z−6=0 is
View SolutionFind the coordinates of the foot of perpendicular drawn from origin to the planes: 5y+8=0
View SolutionFind the coordinates of the foot of perpendicular drawn from origin to the planes: x+y+z=1
View SolutionIn the following cases, find the co-ordinates of the foot of the perpendicular drawn from the origin to the plane :
(i) 2x + 3y + 4z - 12 = 0
(ii) 3y + 4z - 6 = 0
(iii) x + y + z = 1
(iv) 5y + 8 = 0.View SolutionThe foot of the perpendicular drawn from the origin to the plane x+y+z=3 is
View SolutionFind the coordinates of the foot of the perpendicular drawn from the origin to the plane 2x 3y + 4z 6 = 0 .
View Solution