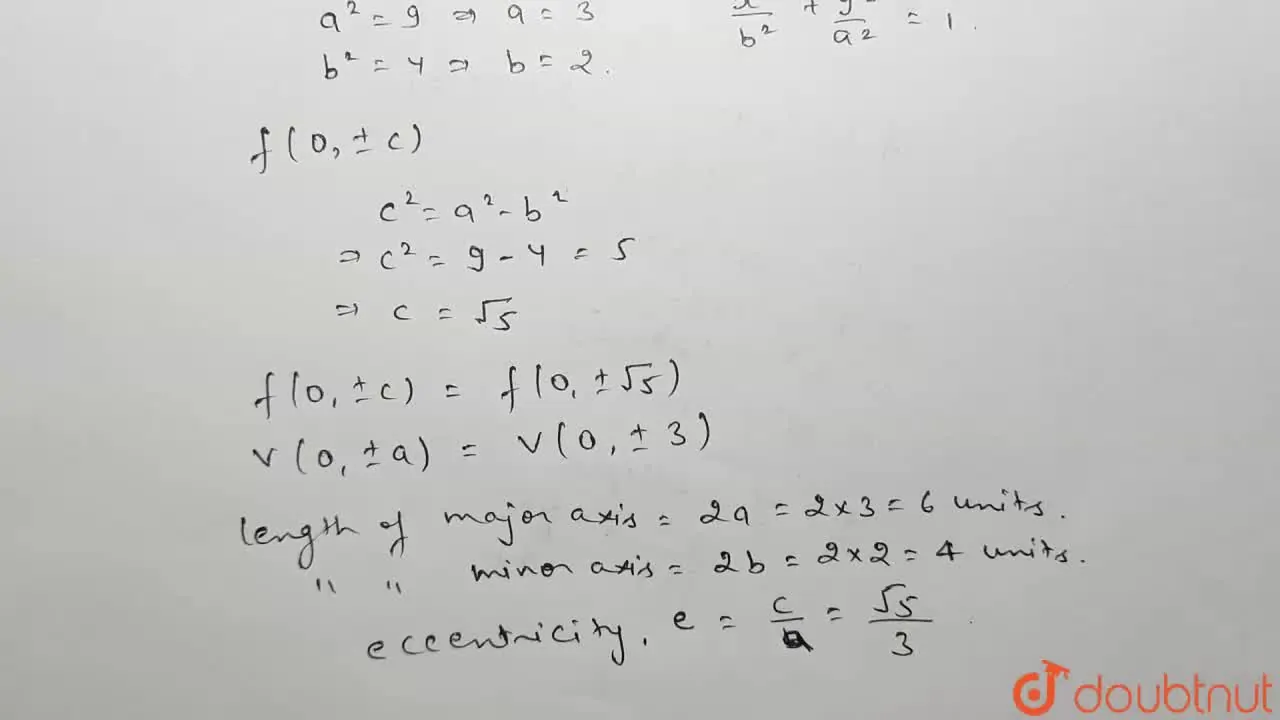Find the coordinates of the foci, the vertices, the lengths of major and minor axes and the eccentricity of the ellipse 9x2+4y2=36.
Given equation is,
9x2+4y2=36
We will convert this equation into standard form.
⇒936x2+436y2=1
⇒x24+y29=1
So, this is our standard equation of ellipse with,
a=2,b=3
c=√b2−a2=√9−4=√5
Here, as b>a, major-axis will be Y−axis.
Now, foci will be (0,±c)=(0,±√5).
Vertices will be (0,±b)=(0,±3).
Length of major-axis =2b=6
Length of minor axis =2a=4
Eccentricity =cb=√53.
Related Playlists
- BOOK - NCERT ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - MISCELLANEOUS EXERCISE9videos
CONIC SECTIONS
- BOOK - NCERT ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - EXERCISE 11.115videos
CONIC SECTIONS
- BOOK - NCERT ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - EXERCISE 11.320videos
CONIC SECTIONS
- BOOK - NCERT ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions75videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
- BOOK - NCERT ENGLISHCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - EXERCISE 12.14videos
INTRODUCTION TO THREE DIMENSIONAL GEOMETRY
Similar Questions
Find the co-ordinates of the foci, the vertices, the lengths of major and minor axes and the eccentricity of the ellipse 16x2+49y2=784.
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the latus rectum of the ellipse x225+y29=1
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.4x2+9y2=36
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.36x2+4y2=144
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.16x2+y2=16
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.x236+y216=1
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.x249+y236=1
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.x216+y29=1
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.x24+y225=1
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.x225+y2100=1
View Solution