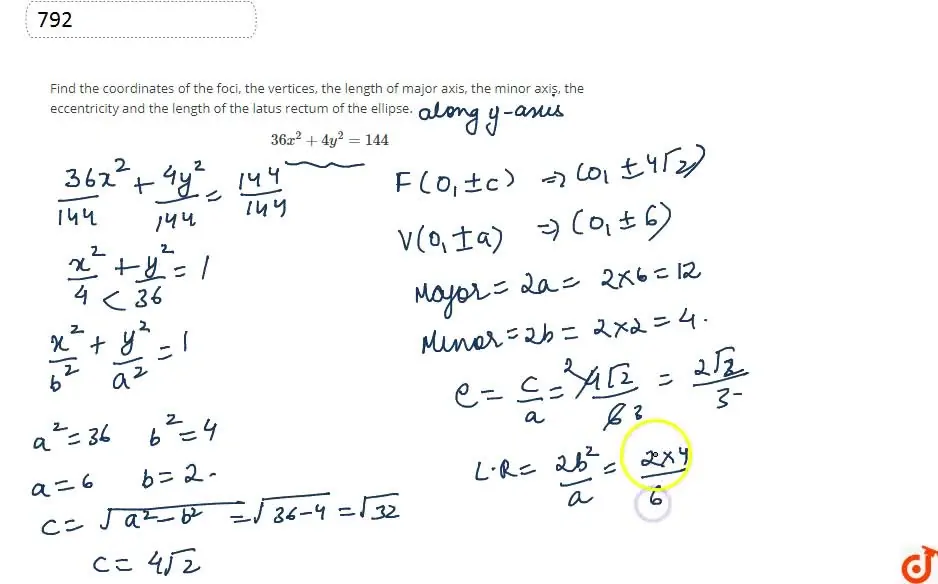Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.36x2+4y2=144
Given equation is,
36x2+4y2=144
We will convert this equation into standard form.
⇒36144x2+4144y2=1
⇒x24+y236=1
So, this is our standard equation of ellipse with,
a=2,b=6
c=√b2−a2=√36−4=√32=4√2
Here, as b>a, major-axis will be Y−axis.
Now, foci will be (0,±c)=(0,±4√2).
Vertices will be (0,±b)=(0,±6).
Length of major-axis =2b=12
Length of minor axis =2a=4
Eccentricity =cb=4√26=2√23.
Length of latus rectum =2a2b=2∗46=43.
Related Playlists
- BOOK - NCERTCHAPTER - CONIC SECTIONSEXERCISE - SOLVED EXAMPLES19videos
CONIC SECTIONS
- BOOK - NCERTCHAPTER - CONIC SECTIONSEXERCISE - EXERCISE 11.414videos
CONIC SECTIONS
- BOOK - NCERTCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - EXERCISE 5.46videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
- BOOK - NCERTCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - EXERCISE 12.14videos
INTRODUCTION TO THREE DIMENSIONAL GEOMETRY
Similar Questions
Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse 36x2+4y2=144
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse x24+y216=1
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.36x2+4y2=144
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse 16x2+y2=16
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse 4x2+9y2=36
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse x216+y29=1
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.16x2+y2=16
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of latus rectum of that ellipses: 9x2+4y2=36
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.4x2+9y2=36
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse x249+y236=1
View Solution