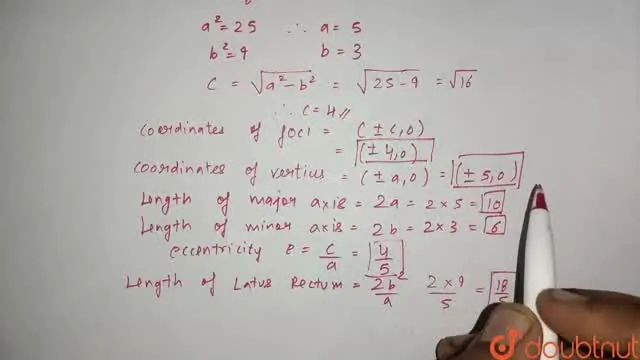Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the latus rectum of the ellipse x225+y29=1

Given equation of ellipse is x24+y225=1
on comparing the given equation with x2a2+y2b2=1, we get
a=2,b=5
since, b>a,∴ the major axis is along the y axis while the minor axis is along the x axis.
Length of major axis=2b=10
length of the minor axis=2a=4
Eccentricity e=√1−a2b2=√25−44=√215
coordinates of the foci are (0,√21) and (0,−√21)
The coordinates of the vertices are (0,5) and (0,−5)
Length of latus rectum=2a2b=2×45=85
Related Playlists
- BOOK - NCERT ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - MISCELLANEOUS EXERCISE9videos
CONIC SECTIONS
- BOOK - NCERT ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - EXERCISE 11.115videos
CONIC SECTIONS
- BOOK - NCERT ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - EXERCISE 11.320videos
CONIC SECTIONS
- BOOK - NCERT ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions75videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
- BOOK - NCERT ENGLISHCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - EXERCISE 12.14videos
INTRODUCTION TO THREE DIMENSIONAL GEOMETRY
Similar Questions
Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.x225+y2100=1
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of latus rectum of that ellipses: x225+y29=1
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.x24+y225=1
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of latus rectum of that ellipses: x225+y2100=1
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.x216+y29=1
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.x236+y216=1
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.x249+y236=1
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.x2100+y2400=1
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.16x2+y2=16
View SolutionFind the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of latus rectum of that ellipses: 25x2+4y2=100
View Solution