Find the coordinates of point on -axis which is equidistant from points and .
Let P(0, y) be the required point and the given points be A (12 , -3) and B (13, 2).
Then PA = PB (given)
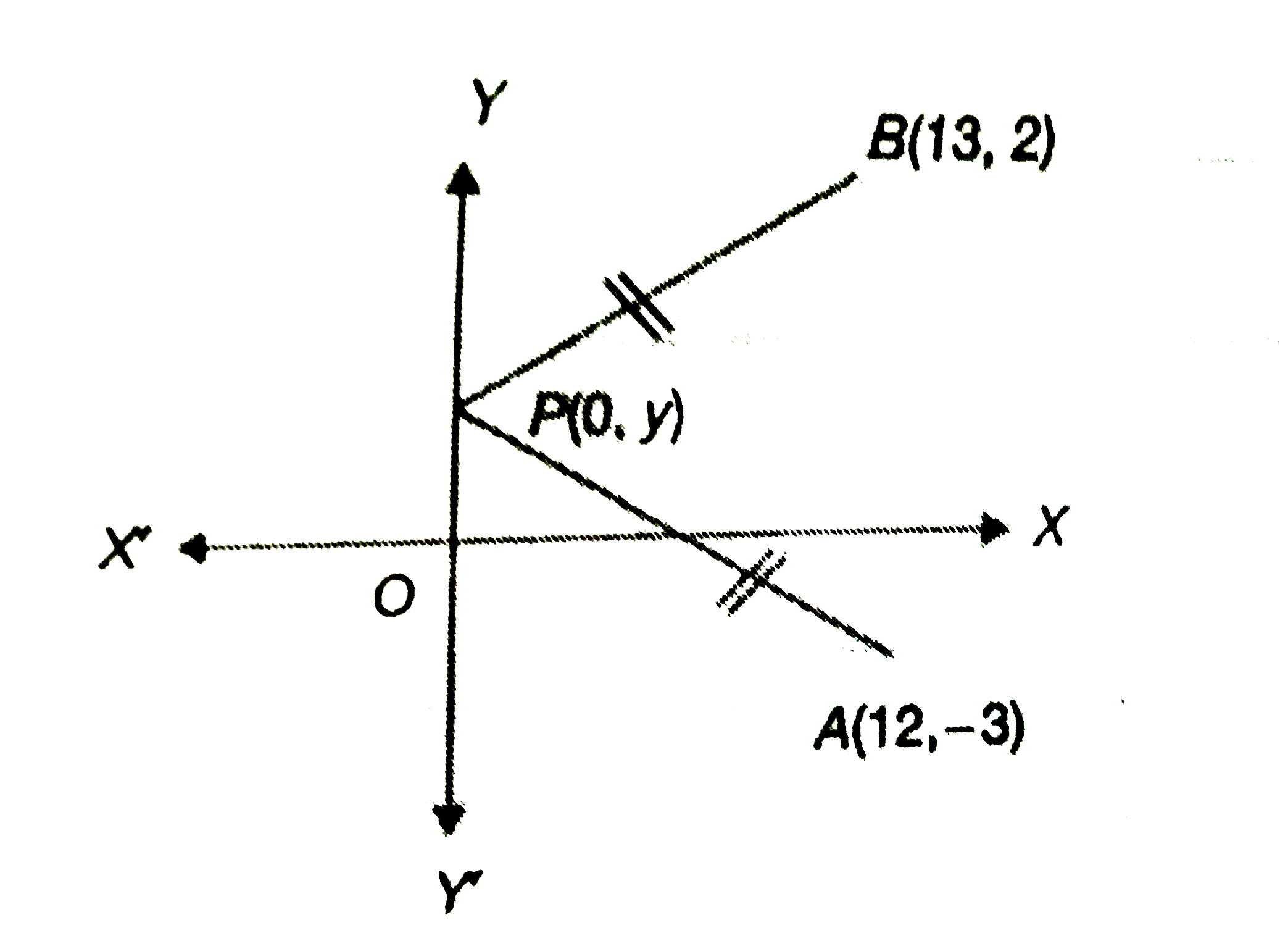
Taking squares on both sides , we get
The required point on Y-axis is (0,2).
Topper's Solved these Questions
- COORDINATE GEOMETRYBook:PEARSON IIT JEE FOUNDATIONChapter:COORDINATE GEOMETRYExercise:Very short Answer Question
Explore 30 Videos
- COORDINATE GEOMETRYBook:PEARSON IIT JEE FOUNDATIONChapter:COORDINATE GEOMETRYExercise:Short Answer Type Questions
Explore 15 Videos
- BANKING AND COMPUTINGBook:PEARSON IIT JEE FOUNDATIONChapter:BANKING AND COMPUTINGExercise:Level 3
Explore 6 Videos
- GEOMETRYBook:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRYExercise:CONCEPT APPLICATION
Explore 61 Videos
Similar Questions
Find the coordinates of a point on y-axis which is equidistant from the points (6, 5) and (-4, 3)
View SolutionWrite the coordinates of a point on X -axis which is equidistant from the points (−3, 4) and (2, 5) .
View SolutionFind the co-ordinates of a point on Y-axis which is equidistant from S (-3,-1) and T (2,-2) .
View SolutionFind the co-ordinates of a point on Y-axis which is equidistant from M(−5,−2)andN(3,2)
View SolutionFind the co-ordinates of a point on Y-axis which is equidistant from M(-5,-2) and N (3,4)
View SolutionFind the coordinates of a point on the x-axis which is equidistant from the points A(2, - 5) and B(- 2, 9).
View SolutionFind a point on y-axis which is equidistant from the points (5, −2) and (−3, 2) .
View SolutionFind the point on Y-axis which is equidistant from the points (−5,2)and(9,−2).
View SolutionFind the point on x-axis which is equidistant from the points (−2, 5) and (2, −3) .
View SolutionWrite the coordinates of a point P on x-axis which is equidistant from the points A(-2, 0) and B(6, 0).
View Solution
