Find the conjugate of (3−2i)(2+3i)(1+2i)(2−i).
Video Solution
Text Solution
The correct Answer is:N/a
Let z=(3−2i)(2+3i)(1+2i)(2−i)
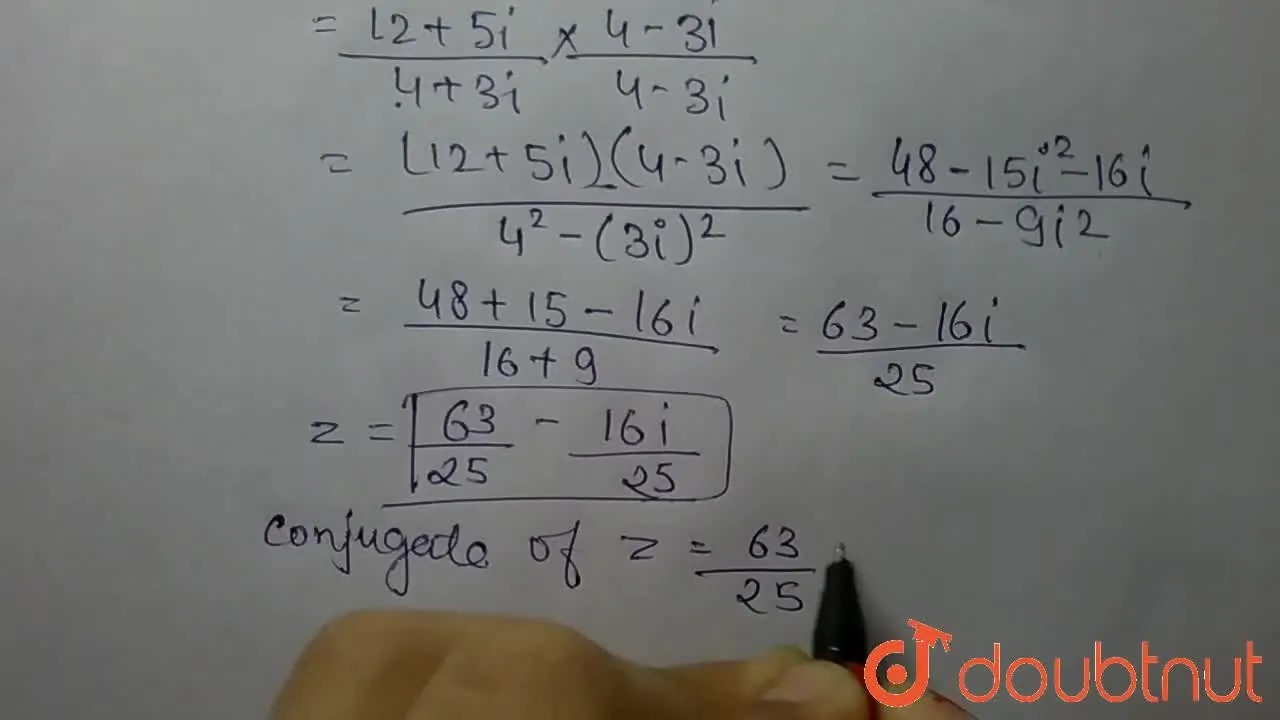
=6−6i2+5i2−2i2+3i=12+5i4+3i
=12+5i4+3i×4−3i4−3i
=48−15i2−16i16−9i2
=63−16i25=6325−1625i
∴ Conjugate of z=6325+1625i.]
|
Updated on:21/07/2023
Related Playlists
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATION EXERCISE - EXERCISE 5A9videos
COMPLEX NUMBERS AND QUADRATIC EQUATION
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATION EXERCISE - EXERCISE 5B29videos
COMPLEX NUMBERS AND QUADRATIC EQUATION
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Miscellaneous Exericse20videos
BINOMIAL THEOREM
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CONIC SECTIONEXERCISE - Miscellaneous Exercise8videos
CONIC SECTION
Similar Questions
Find the conjugate of
12+5iView SolutionFind the conjugate of (1−2i)22+i
View SolutionThe conjugate of 11−2i is
View SolutionFind the conjugate of 13+4i.
View SolutionThe conjugate of (1+2i)23−i is
View SolutionWrite the conjugate of
(3+4i)2View SolutionWrite the conjugate of 2−i(1−2i)2 .
View SolutionWhat is the conjugate of 2−i(1−2i)2?
View SolutionFind the modulus of (3+2i)24−3i
View SolutionFind the conjugates of the following complex number: (3−2i)(2+3i)(1+2i)(2−i)
View Solution