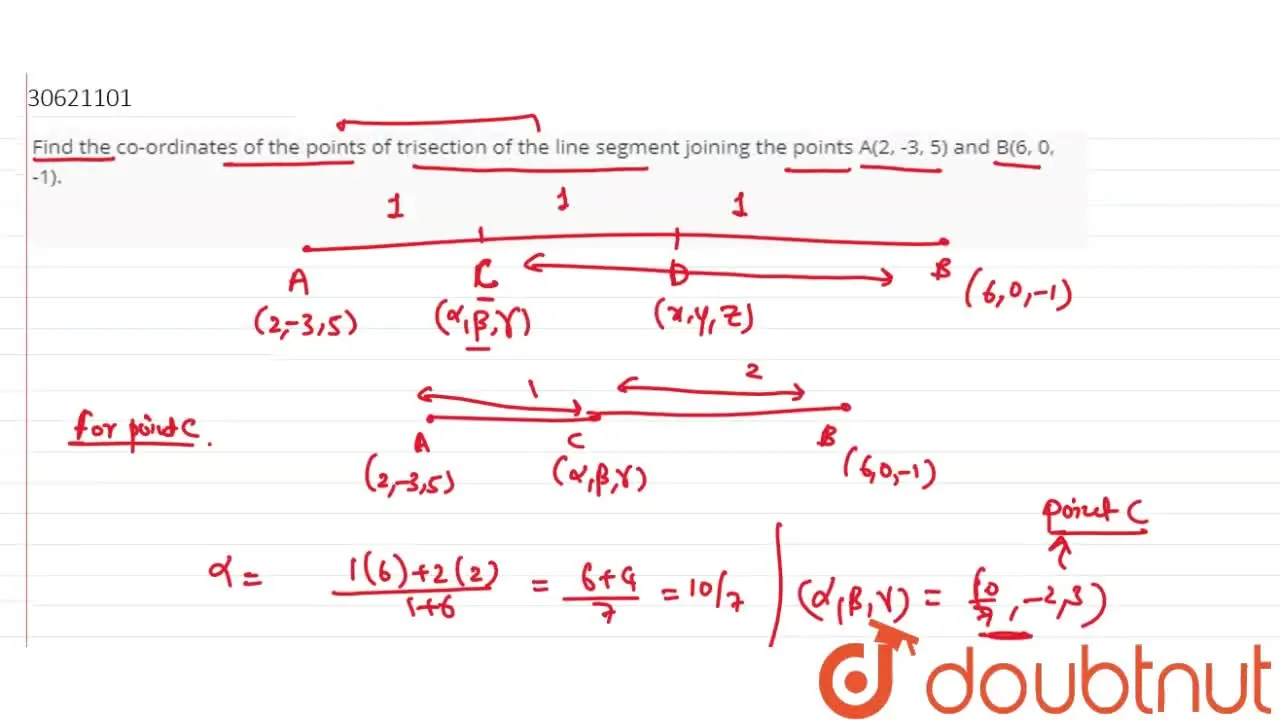
Find the co-ordinates of the points of trisection of the line segment joining the points A(2, -3, 5) and B(6, 0, -1).
The correct Answer is:N/a
Let C(x,y,z) and D(a,b,c) trisect AB.
∴C divides the line segment AB in the ration 1 : 2.
Therefore, x=1×6+2×21+2=103
y=1×0+2×(−3)1+2=−2
z=1×(−1)+2×51+2=3

Similarly, D divides the line segment AB in the ration 2 : 1.
a=2×6+1×22+1=−143
b=2×0+1×(−3)2+1=−1
c=2×(−1)+1×52+1=1
∴ Co-ordinates of the points of trisection are C(103,−2,3) andD(143,−1,1)
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION OF THREE DIMENSIONAL GEOMETRYEXERCISE - Exercise 12 A5videos
INTRODUCTION OF THREE DIMENSIONAL GEOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION OF THREE DIMENSIONAL GEOMETRYEXERCISE - Exercise 12 B18videos
INTRODUCTION OF THREE DIMENSIONAL GEOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - CONIC SECTIONEXERCISE - Miscellaneous Exercise8videos
CONIC SECTION
- BOOK - NAGEEN PRAKASHANCHAPTER - LIMITS AND DERIVATIVESEXERCISE - Miscellaneous Exercise30videos
LIMITS AND DERIVATIVES
Similar Questions
Find the co-ordinates of the points of trisection of the line segment joining the points (2, 5) and (6, -2).
View SolutionFind the coordinates of the points of trisection of the line segment joining the points A(-5, 6) and B(4, -3).
View SolutionFind the coordinates of the points of trisection of the line segment joining the points A(7, -2) and B(1, 5).
View SolutionFind the co-ordinates of the points of trisection of the line segment joining the points A(−5,6)andB(4,−3).
View SolutionFind the co-ordinates of the points fo trisection of the line segment joining the points (-2, 0) and (4, 0).
View SolutionFind the co-ordinates of the point of bisection of the line segment joining the points (9, -3) and (9,7).
View SolutionFind the coordinates of the points of trisection of the line segment joining the points (2,-2) and (-7,-4)
View SolutionFind the coordinates of the points of trisection of the line segment joining (4, 1) and (2, 3).
View SolutionFind the co - ordinates of the points of trisection of the line segment joining (4,−1) and (−2,−3).
View SolutionFind the coordinates of the points which trisect the line segment joining the points (2,3)and(6,5).
View Solution