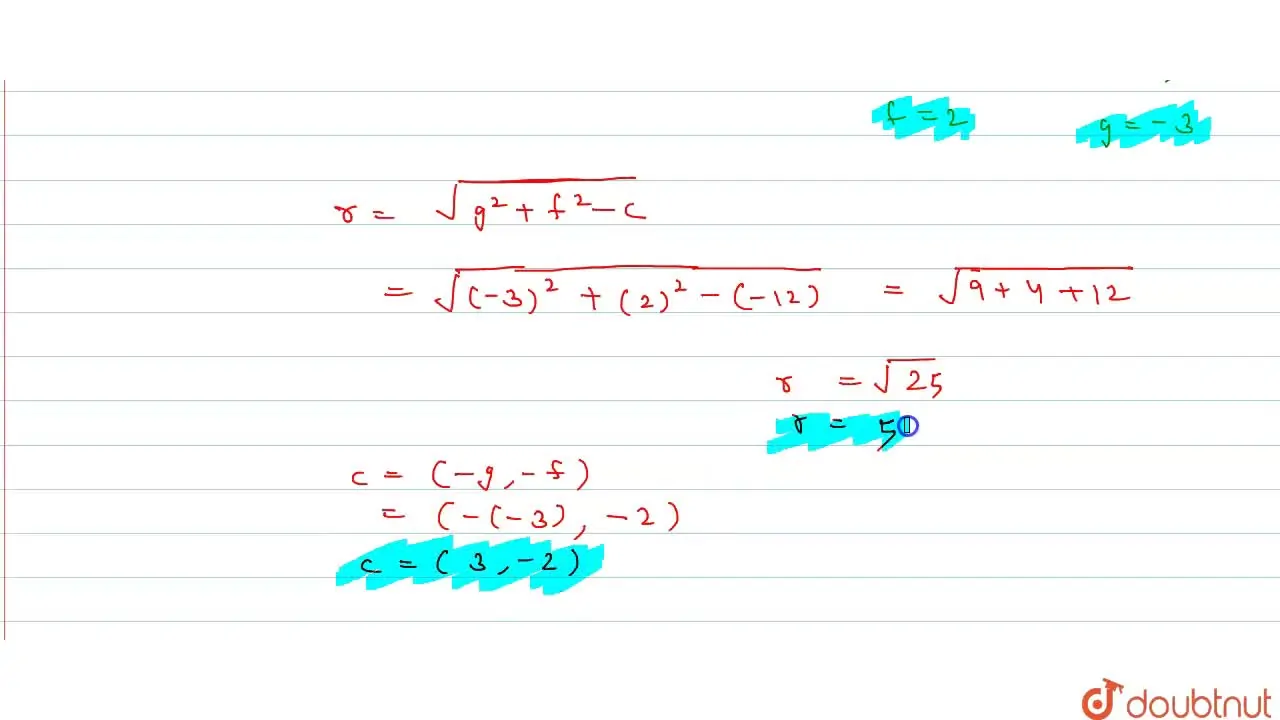Find the centre and radius of the circle x2+y2−6x+4y−12=0.
Video Solution
Text Solution
On comparing the give equation with the general equation of the circle
i.e., x2+y2+2gx+2fy+c=0
we get, 2g=−6,2f=4 and c=−12
⇒g=−3,f=2 and c=−12
∴ The co-ordinates of the centre of the circle is (−g,−f) i.e., (3,−2) and the radius is √g2+r2−c
i.e, √(−3)2+(2)2−(−12)=√25 or 5.
|
Updated on:21/07/2023
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - CONIC SECTIONSEXERCISE - Try ypurself42videos
CONIC SECTIONS
- BOOK - AAKASH INSTITUTECHAPTER - CONIC SECTIONSEXERCISE - Assignment (SECTION - A)55videos
CONIC SECTIONS
- BOOK - AAKASH INSTITUTECHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - section-J (Aakash Challengers Qestions)16videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
- BOOK - AAKASH INSTITUTECHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - section - J6videos
CONTINUITY AND DIFFERENTIABILITY
Similar Questions
Find the centre and radius of the circle x2+y2+6x−10y−2=0
View SolutionFind the centre and radius of the circle 3x2+3y2−6x+9y−8=0.
View SolutionFind the centre and radius of the circles : x2+y2−2x+4y=8
View SolutionFind the co-ordinates of the centre and radius of the circle
3x2+3y2+6x+4y−3=0View SolutionFind the centre and radius of the circle 4x2+4y2+16y−4x=19.
View SolutionFind the centre and radius of the circles : x2+y2−ax−by=0
View SolutionFind the centre and radius of the circle x2+y2+2x−4y−4=0
View SolutionFind the centre and radius of the circle 3x2+3y2−8x−10y+3=0
View SolutionCentre and radius of circle 2x2+2y2−6x+4y−3=0 are
View SolutionFind the centre and radius of the circles : x2+y2−8x−12y−48=0
View Solution