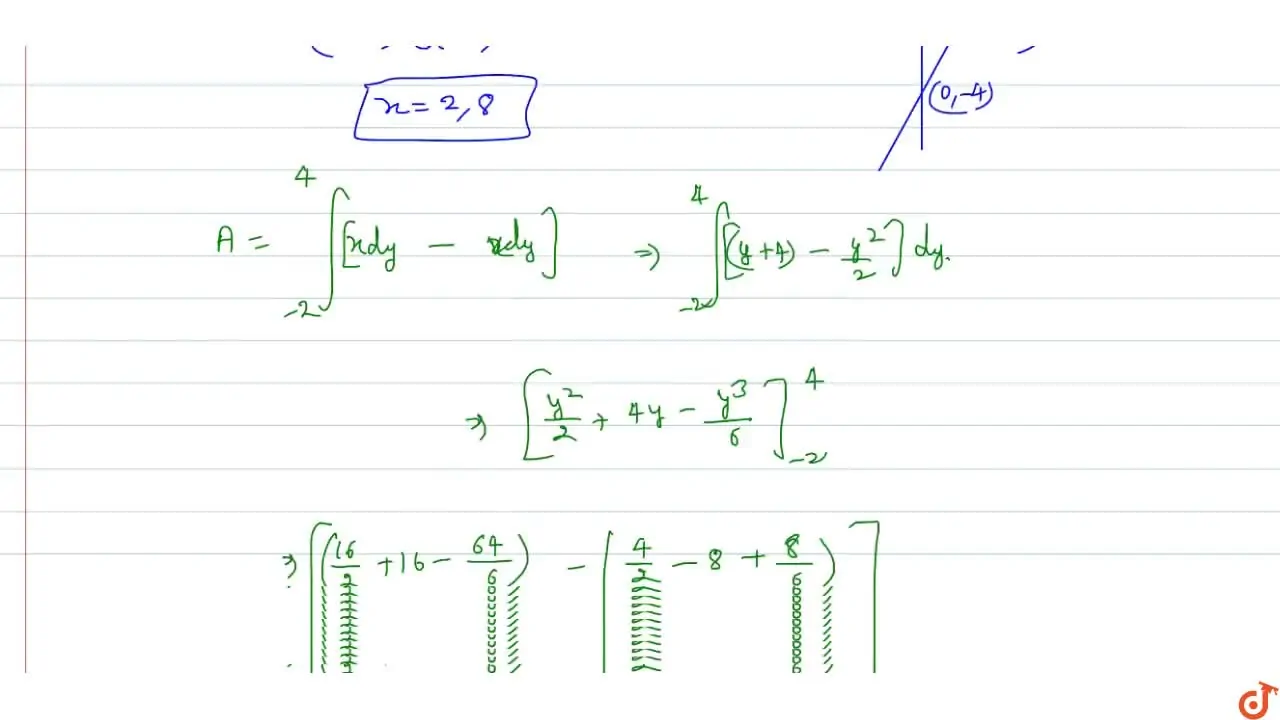
Find the area of the region bounded by the parabola y2=2x and straight line x−y=4.
The intersecting points of the given curves are obtained by solving the equations x–y=4 and y2=2x for x and y.
We have y2=8+2y
i.e (y–4)(y+2)=0 which gives y=4,–2and x=8,2.
Thus, the points of intersection are (8,4),(2,–2). Hence ,
Area=∫4−2(4+y−12y2)dy
=∣∣∣4y+y22−y36∣∣∣4−2
=18 sq units
Related Playlists
Similar Questions
Find the area of the region bounded by the parabola y=x2 and y=|x|.
View SolutionFind the area of the region bounded by the parabola y=x2 and y=|x| .
View SolutionUsing integration, find the area of the region bounded by the parabola y2=16x and the line x=4
View SolutionFind the area of the region bounded by the parabola y2=2x and the line x−y=4
View SolutionUsing integration, find the area of the region bounded by the parabola y2=4x and the line x=4.
View SolutionFind by the method of integration the area of the region bounded by the parabola y2=16x and the line x=5.
View SolutionFind the area of the region bounded by the parabola y2=25x and the line x =5
View SolutionFind the area of the region bounded by the parabola y2=16x and the line x=4.
View SolutionFind the area of the region bounded by the parabola y2=8x and the line x=2
View SolutionFind the area of the regions bounded by the parabola y2=4ax and the line x=a.
View Solution