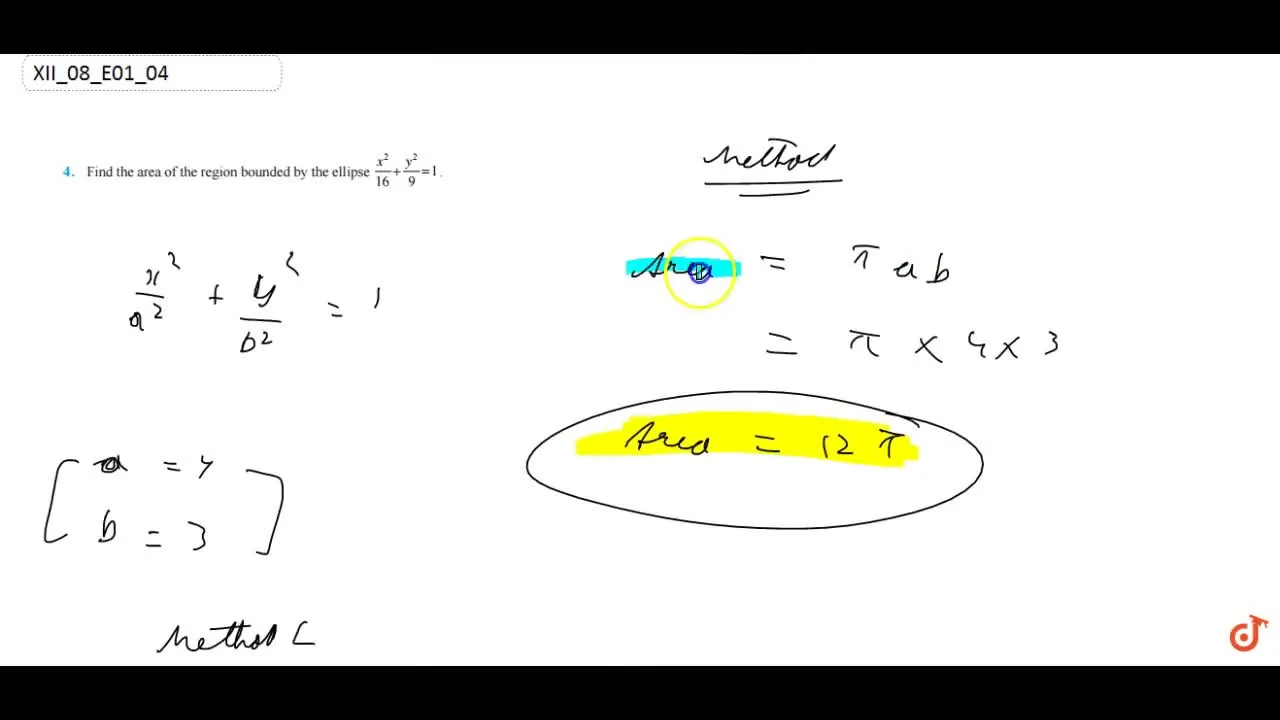
Find the area of the region bounded by the ellipse x216+y29=1.
10π
11π
12π
13π
The correct Answer is:C
x216+y29=1
y29=16−x216
y2=916(16−x2)
y=±34√16−x2
I=4∫40ydx
=4∫40√16−x2
=3(12x√16−x2+162sin−1x4)40
=3(42√16−16+162sin−1(44)−0−0)
=3⋅162sin−1
=12π
Related Playlists
- BOOK - NCERTCHAPTER - APPLICATION OF INTEGRALSEXERCISE - MISCELLANEOUS EXERCISE19videos
APPLICATION OF INTEGRALS
- BOOK - NCERTCHAPTER - APPLICATION OF INTEGRALSEXERCISE - SOLVED EXAMPLES15videos
APPLICATION OF INTEGRALS
- BOOK - NCERTCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - EXERCISE 6.118videos
APPLICATION OF DERIVATIVES
- BOOK - NCERTCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - QUESTION3videos
CONTINUITY AND DIFFERENTIABILITY
Similar Questions
Find the area of the region bounded by the ellipse x24+y29=1
View SolutionFind the area of the region bounded by the ellipse x29+y24=1 in fourth quadrant.
View SolutionFind the area of the region bounded by the ellipse x24+y29=1.
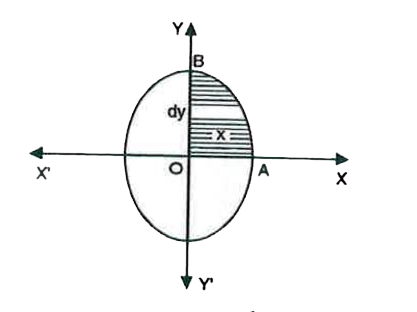 View Solution
View SolutionFind the area of the region bounded by the ellipse x2a2+y2b2=1
View SolutionFind the area of the region bounded by the ellipse x29+y24=1 in fourth quadrant.
View SolutionUsing definite integration, find the area of the smaller region bounded by the ellipse 9x2+16y2=144andx=2.
View SolutionFind the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1
View SolutionFind the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1.
View SolutionThe area of the region bounded by the ellipse x225+y216=1 is
View SolutionThe area of the region bounded by the ellipse x225+y216=1 is
View Solution