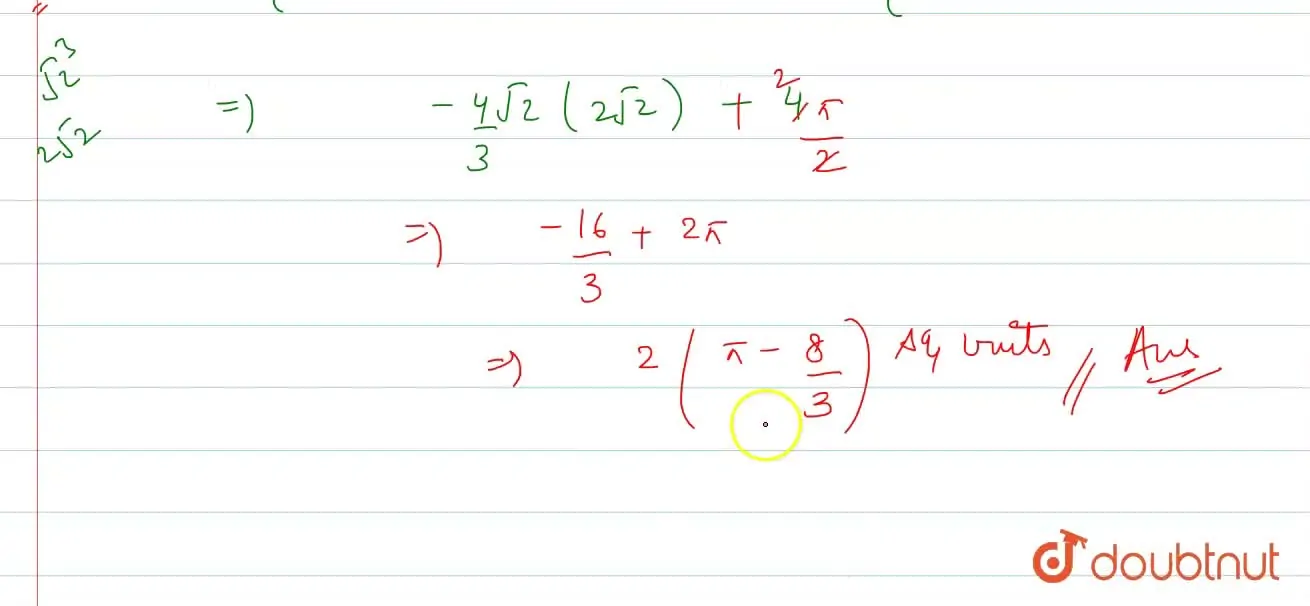Find the area of the region bounded by the curve y2=2x and x2+y2=4x.
Video Solution
Text Solution
The correct Answer is:N/a
We have, y2=2x and x2+y2=4x
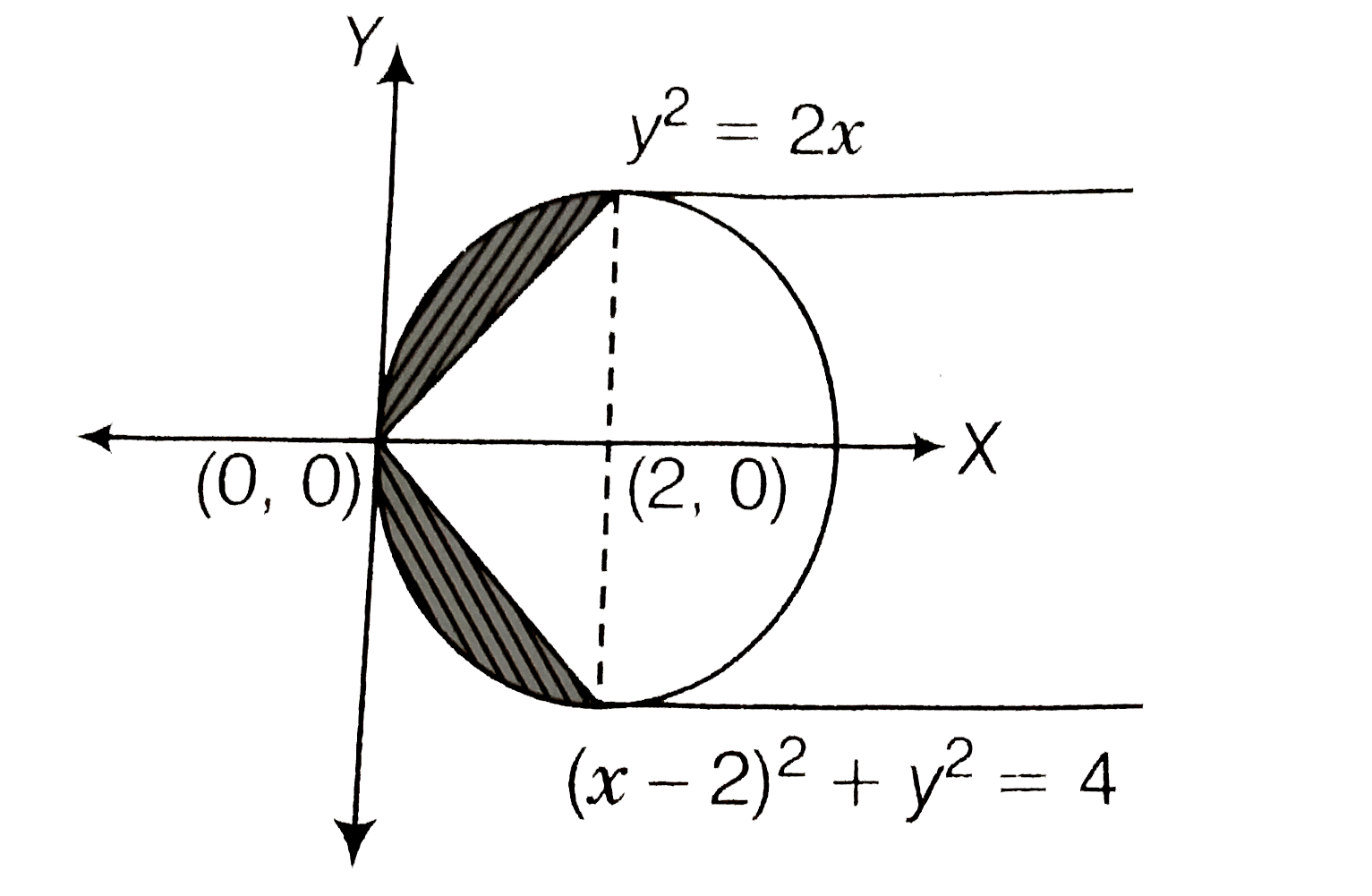
⇒x2+2x−4x
⇒x2−2x=0
⇒x(x−2)=0
⇒x=0,2
Also, x2+y2=−y2
⇒x2−4x=−y2
⇒x2−4x+4=−y2+4
⇒(x−2)2−292)=−y2
∴ Required area =2.∫20[√22−(x−2)2−√2x]dx
=2⎡⎣[x−22.√22−(x−2)2+222sin−1(x−22)]20−[√2.x3/23/2]20⎤⎦
=2[(0+0−1.0+3.π2)−2√23(23/2−0)]
=4π2−8.23=2π−163=2(π−83) sq units
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Find the area of the region bounded by the curve y2=4x and x2=4y.
View SolutionFind the area of the region bounded by the curve y2=4x and x2=4y.
View SolutionFind the area of the region bounded by the curve y2=9x and y=3x.
View SolutionFind the area of the region bounded by the curve y2=9x and y=3x.
View SolutionFind the area of the region bounded by the curves y2=4ax and x2=4ay.
View SolutionThe area of the region bounded by the curves y=x2 and x=y2 is
View SolutionThe area of the region bounded by the curves x=y2−2 and x=y is
View SolutionFind the area of the region bounded by the curves y2=x+1 and y2=−x+1.
View SolutionExamples: Find the area of the region bounded by the curve y2=2y−x and the y-axis.
View SolutionFind the area of the region bounded by the curves x2+y2=4 and (x−2)2+y2=4.
View Solution