Find the area of the quadrilateral formed by common tangents drawn from a point P to the circle x2+y2=8 and the parabola y2=16x, chord of contact of tangents to the circle and chord of contact of tangents to the parabolas.
Let any tangent to the parabola y2=8x be y=mx+4m. It also touches the circle x2+y2=8
∴ Length of perpendicular from centre of the circle to the line = radius of the circle.
⇒∣∣
∣∣0−0+4m√1+m2∣∣
∣∣=2√2

(4m)2=8+8m2
m2+m2−2=0
(m2+2)(m2−1)=0
m=±1
∴ The common tangents are
y=x+4andy=−x−4
Point of intersection of these tangents is P(−4,0) Equation of chord of contact to the circle from P(−4,0) is
−4x+0=8⇒x+2=0
Equation of chord of contact of tangents to the parabola is
0=4(x−4)
⇒x−4=0
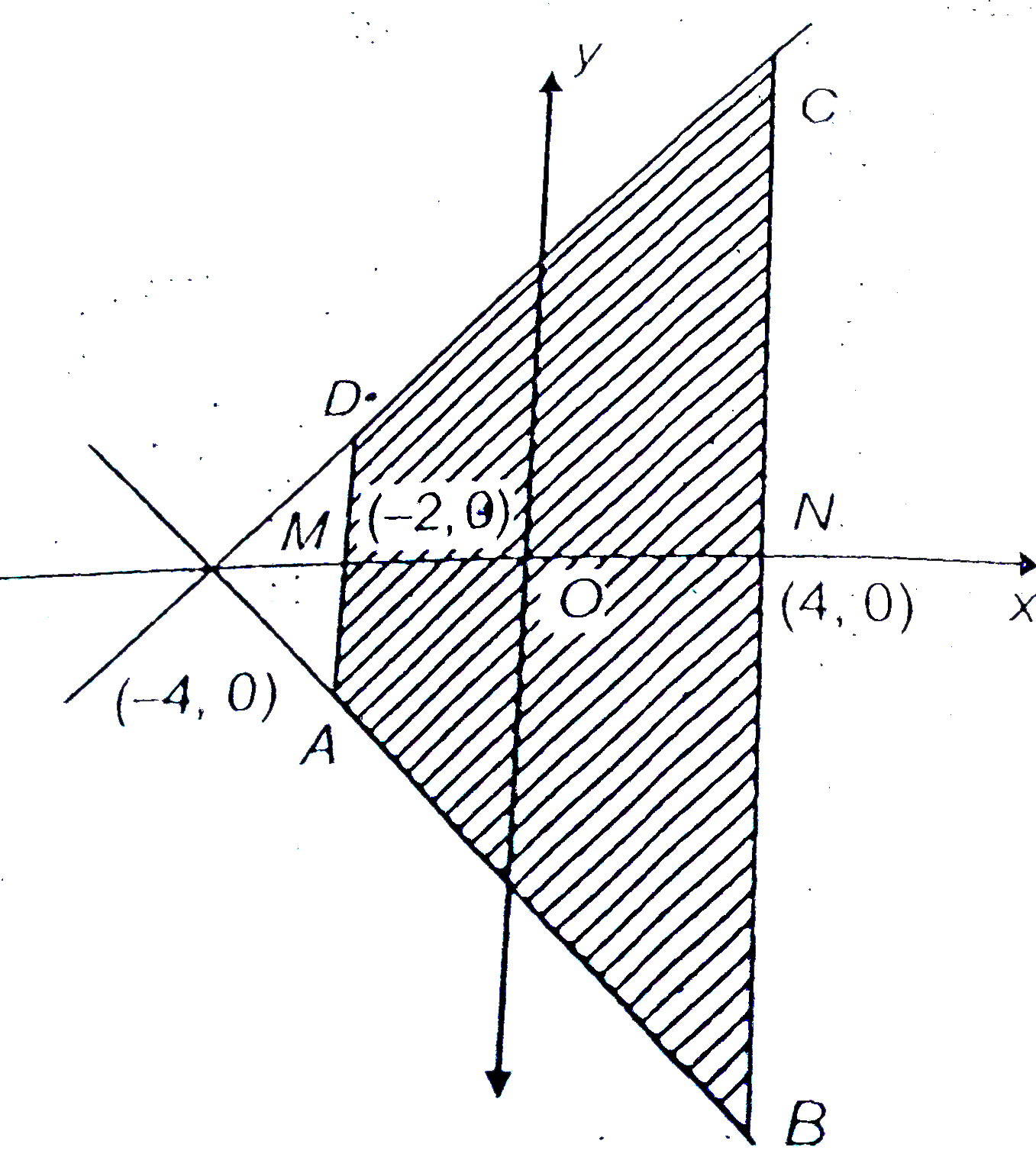
Redrawing the figure formed by four lines, we require the area of the shaded region i.e., trapezium
Required area =12(AD+BC)×MN
=12(4+16)×6
=60 sq. units
Related Playlists
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - Try ypurself42videos
CONIC SECTIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - Assignment (SECTION - A)55videos
CONIC SECTIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - section-J (Aakash Challengers Qestions)13videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - section - J6videos
CONTINUITY AND DIFFERENTIABILITY
Similar Questions
Find the area of the triangle formed by two tangents drawn from (3,5) to the circle x2+y2=16 and the chord of contact of (3,5)
View SolutionEquation of a common tangent to the circle x2+y2−6x=0 and the parabola y2=4x is
View SolutionFind the equations of the common tangents to the circle x2+y2=8 and the parabola y2=16x.
View SolutionFind the area of the triangle formed by the tangents drawn from the point (4,6) to the circle x2+y2=25 and their chord of contact.
Answer: 405√352 sq. unitsView SolutionAngle between tangents drawn from a points P to circle x2+y2−4x−8y+8=0 is 60∘ then length of chord of contact of P is
View Solutionfind the common tangents of the circle x2+y2=2a2 and the parabolay2=8ax
View SolutionIf two tangents are drawn from a point to the circle x2+y2=32 to the circle x2+y2=16, then the angle between the tangents is
View SolutionThe area of the triangle formed by the tangents from (1,3) to the circle x2+y2−4x+6y+1=0 and its chord of contact is
View SolutionTangent are drawn from the point (3, 2) to the ellipse x2+4y2=9 . Find the equation to their chord of contact and the middle point of this chord of contact.
View SolutionFind the area of the triangle formed by the tangents from the point (4, 3) to the circle x2+y2=9 and the line joining their points of contact.
View Solution


