Find the area of a quadrilateral ABCD whose vertices are A(-4, 8), B(-3, -4), C(0, -5) and D(5, 6).

Video Solution

Text Solution

Verified by Experts

Area of quad. ABCD = $a r (Δ A B C) + a r (Δ A C D) .$

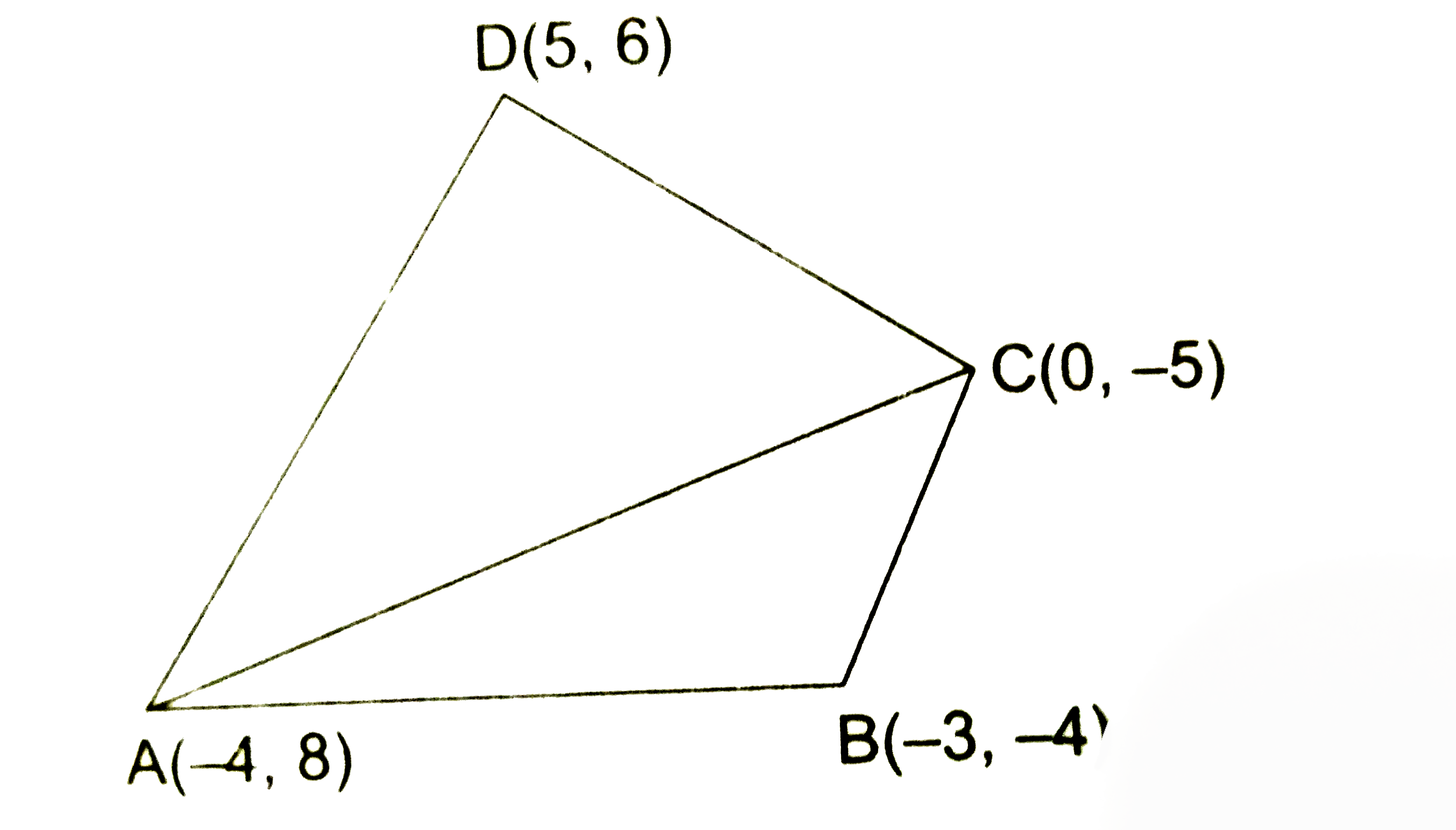
For $Δ A B C$ , we have
$(x_{1} = - 4, y_{1} = 8), (x_{2} = - 3, y_{2} = - 4) and (x_{3} = 0, y_{3} = - 5)$
$∴ a r (Δ A B C) = \frac{1}{2} | x_{1} (y_{2} - y_{3}) + x_{2} (y_{3} - y_{1}) + x_{3} (y_{1} - y_{2}) |$
$= \frac{1}{2} | (- 4) \cdot (- 4 + 5) + (- 3) \cdot (- 5 - 8) + 0 \cdot (8 + 4) |$
$= \frac{1}{2} | (- 4) \times 1 + (- 3) \times (- 13) + 0 |$
$= \frac{1}{2} | - 4 + 39 + 0 | = \frac{35}{2}$ sq units.
For $Δ A C D$ , we have
$(x_{1} = - 4, y_{1} = 8), (x_{2} = 0, y_{2} = - 5) and (x_{3} = 5, y_{3} = 6) .$
$∴ a r (Δ A C D) = \frac{1}{2} | x_{1} (y_{2} - y_{3}) + x_{2} (y_{3} - y_{1}) + x_{3} (y_{1} - y_{2}) |$
$= \frac{1}{2} | (- 4) \cdot (- 5 - 6) + 0 \cdot (6 - 8) + 5 \cdot (8 + 5) |$
$= \frac{1}{2} | (- 4) \times (- 11) + 0 \times (- 2) + 5 \times 13 |$
$= \frac{1}{2} | 44 + 0 + 65 | = \frac{109}{2}$ sq unit.
$∴ a r (quad . A B C D) = a r (Δ A B C) + a r (Δ A C D)$
$= (\frac{35}{2} + \frac{109}{2}) sq units = \frac{144}{2}$ sq units
= 72 sq units.
Hence, the area of the given quadrilateral ABCD is 72 sq units.

Updated on:21/07/2023

|

Class 10 MATHS COORDINATE GEOMETRY

Topper's Solved these Questions

Similar Questions

RS AGGARWAL-COORDINATE GEOMETRY-Multiple Choice Questions (Mcq)

Home
Ask Doubt
Profile