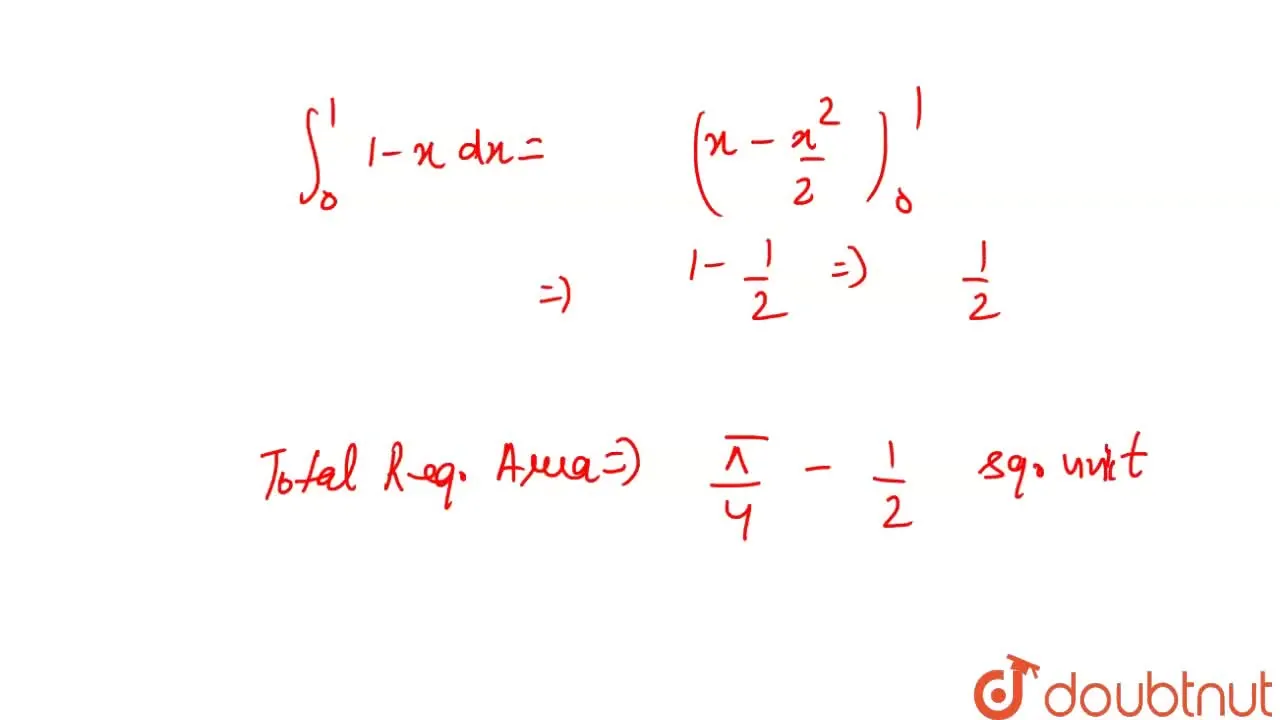Find the area enclosed between the circle x2+y2=1 and the line x+y=1 lying in the first quadrant.

Required area = area of the region ACBDA
= (area of the region OACBO) - (area of the region OADBO)
Now, area of the region OACBO = area under the circle x2+y2=1
=∫10ydx, where y2=1−x2, i.e., y=√1−x2, as y>0
=∫10√1−x2dx=[x2√1−x2+12sin−1(x)]10
=12√1−1+12sin−11−0=12×π2=π4
Area of the region OADBO = area under the line x+y=1
=∫10ydx, where y=1−x=∫10(1−x)dx=[x−x22]10=1−12−0=12
∴ required area = π4−12=12(π2−1) sq units.
Related Playlists
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS ( AREA ) EXERCISE - EXAMPLES FOR PRACTICE (2 MARKS )8videos
APPLICATIONS OF DEFINITE INTEGRALS ( AREA )
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS ( AREA ) EXERCISE - EXAMPLES FOR PRACTICE (3 OR 4 MARKS )5videos
APPLICATIONS OF DEFINITE INTEGRALS ( AREA )
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - APPLICATIONS OF DERIVATIVES EXERCISE - MULTIPLE CHOICE QUESTIONS12videos
APPLICATIONS OF DERIVATIVES
Similar Questions
Find the area enclosed by the circle x2+y2=9.
View SolutionFind the area enclosed between the circle x2+y2=9 , along X – axis and the line x = y , lying in the first quadrant.
View SolutionFind the area enclosed between the circle x2+y2=25 and the straight line x+y=5.
View SolutionFind the area enclosed by the circle x2+y2=25
View SolutionFind the smaller area enclosed by the circle x2+y2=4 and the line x+y=2.
View SolutionFind the area enclosed by the circle x2+y2=a2.
View SolutionFind the area enclosed between first quadrant of a circle x2+y2=16 and line y=x.
View SolutionArea enclosed between the curve y=x2 and the line y = x is
View SolutionFind the area enclosed between curve y=x2+2, x-axis, x=1 and x=2.
View SolutionFind the smaller area enclosed by the circle x2+y2=4 and the line x+y=2.
View Solution