Find the area bounded by the cirxle x2+y2=16 and the line y=x in the first quadrant .
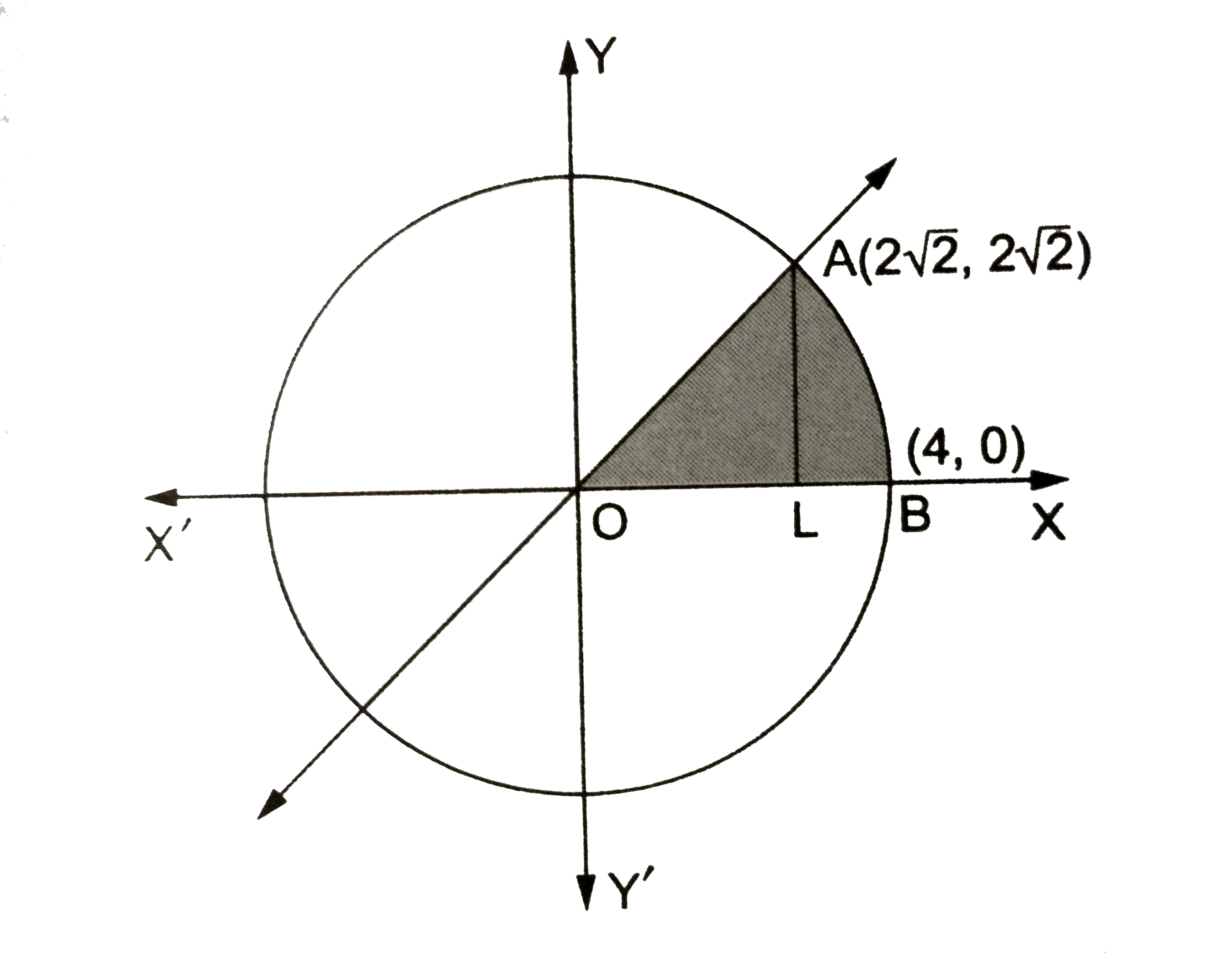
Putting y = x from (ii) into (i) we get
2x2=16⇔x8⇔x=2√2 [ ∴ x is + ve in the first quad ]
Thus the point of intersection of (i) and (ii) in the first quadrant is A(2√2,2√2
Draw AL perpendicular on the x-axis
∴ required area= (area OLA )+ area (LBAL)
=2√2∫0xdx+4∫2√2√16−x2dx
=[x22]−2√20+[x√16−x22+162sin−1x4]42√2
12[(2√2)2−0]+[(0+8sin−1)−4+8sin−11√2]
=[4+(8×π2)−4−(8×π4)]=(2π) sq units
Related Playlists
- BOOK - RS AGGARWALCHAPTER - AREA OF BOUNDED REGIONS EXERCISE - Exercise 1739videos
AREA OF BOUNDED REGIONS
- BOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Objective Questions89videos
APPLICATIONS OF DERIVATIVES
- BOOK - RS AGGARWALCHAPTER - BAYES'S THEOREM AND ITS APPLICATIONSEXERCISE - Exercise 3018videos
BAYES'S THEOREM AND ITS APPLICATIONS
Similar Questions
Find the area bounded by the circle x2+y2=16 and the line √3y=x in the first quadrant, using integration.
View SolutionThe area bounded by the circle x2+y2=a2 and the line x+y=a in the first quadrant is
View SolutionFind the area bounded by the curve y=x2+2x−3 and the line y=x+3.
View SolutionThe area bounded by the curve y2=16x and the line x = 4 is
View SolutionFind the area enclosed between circle x2+y2=1 and the line x+y=1 in first quadrant.
View SolutionFind the area bounded by the parabola y=x2 and the line y−2x=2.
View SolutionFind the area bounded by the curve y2=36x, the line x = 2 in first quadrant .
View SolutionThe area bounded by the curve y2=9x and the lines x=1,x=4andy=0, in the first quadrant,is
View SolutionFind the area of sector bounded by the circle x2+y2=25 , in the first quadrant.
View SolutionWhat is the area bounded by the curve y=x2 and the line y=16?
View Solution


