Find the area bounded by curve y=x2−1 and y = 1 .
Video Solution
Text Solution
A1≡y=x2−1
A2≡y=1
Curve is
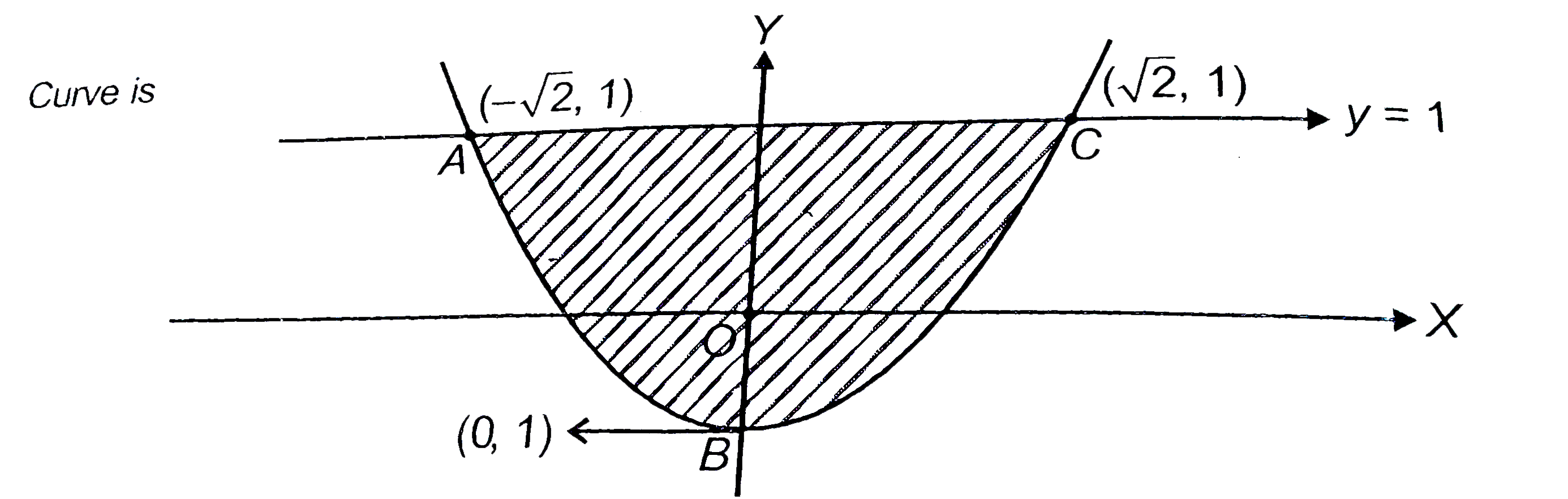
Required area = area of ABCA
=√2∫−√2(1−x2+1)dx
=2√2∫0(2−x2) dx
=2(2x−x33)√20
=2(2√2−2√23) sq. unit
=8√23 sq. unit
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - APPLICATION OF INTEGRALS EXERCISE - Try Yourself4videos
APPLICATION OF INTEGRALS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - APPLICATION OF INTEGRALS EXERCISE - Assignment Section - A Competition Level Questions24videos
APPLICATION OF INTEGRALS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Assignment SECTION-J (Aakash Challengers Questions )8videos
APPLICATION OF DERIVATIVES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Assignment (section-J) Objective type question (Aakash Challengers Questions)4videos
BINOMIAL THEOREM
Similar Questions
Find the area bounded by the curves x=∣∣y2−1∣∣ and y=x−5
View SolutionUsing integration, find the area bounded by the curves y=|x−1| and y=3−|x|.
View SolutionUsing integration, find the area bounded by the curves y=|x−1| and y=3−|x|.
View SolutionFind the area bounded by the curves y=6x−x2andy=x2−2x
View SolutionFind the area bounded by the curve y=x2,y=(x−2)2 and the axis .
View SolutionFind the area bounded by the curves x=y2 and x=3−2y2.
View SolutionArea bounded by the curves y=x2−1andx+y=3 is:
View SolutionFind the area bounded by curves −4y2=x and x=1+5y2
View SolutionThe area bounded by the curves y = |x| - 1 and y=−|x|+1 is equal to
View SolutionFind the area bounded by curves {(x,y):y≥x2andy=|x|}
View Solution
