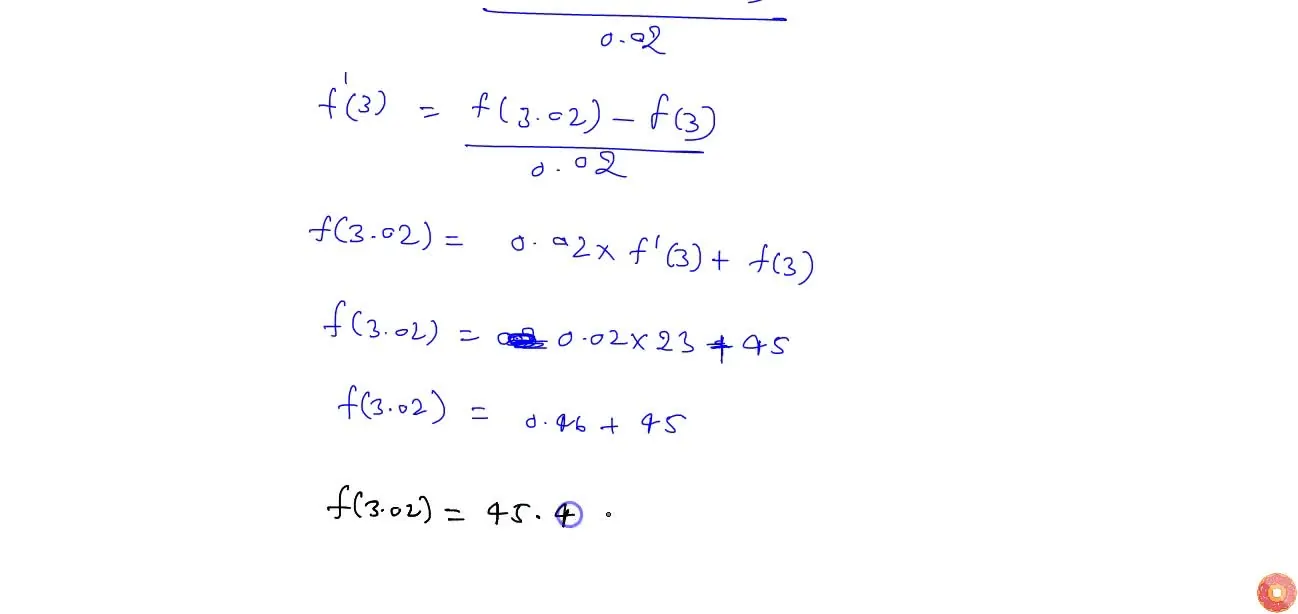Find the approximate value of f(3.02), upto 2 places of decimal, where f(x)=3x2+5x+3.
Video Solution
Text Solution
Here, we will use the definition of derivatives:
f'(x)=f(x+Δx)−f(x)(x+Δx)−x
f'(x)=f(x+Δx)−f(x)Δx
Here, x=3andΔx=0.02
∴f'(3)=f(3+0.02)−f(3)0.02→(1)
Here, f'(x)=6x+5
∴f'(3)=6(3)+5=23
f(3)=3(9)+5(3)+3=45
So,putting these values in (1),
23=f(3.02)−450.02
0.46+45=f(3.02)
⇒f(3.02)=45.46
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Find the approximate value of f(3.02) , where f(x)=3x2+5x+3 .
View SolutionFind the approximate value of f(3.02), where f(x)=3x2+5x+3.
View SolutionFind the approximate value of f(3.02), where f(x)=3x2+5x+3.
View SolutionFind the approximate value of f(2.01) , where f(x)=4x2+5x+2 .
View SolutionFind the approximate value of f(3.02), where f(x)=3x2+15x+5.
View SolutionFind the approximate value of f(3.12), where f(x)=4x2+5x+2.
View SolutionFind the approximate value of f(2.01) where f(x)=x3−4x+7.
View SolutionFind the approximate value of :
f(3.02), where f(x)=3x2+15x+3View SolutionFind the approximate value of f(5.001) , where f(x)=x3−7x2+15 .
View SolutionFind the approximate value of f(2.01), where f(x)=4x2+5x+2.
View Solution