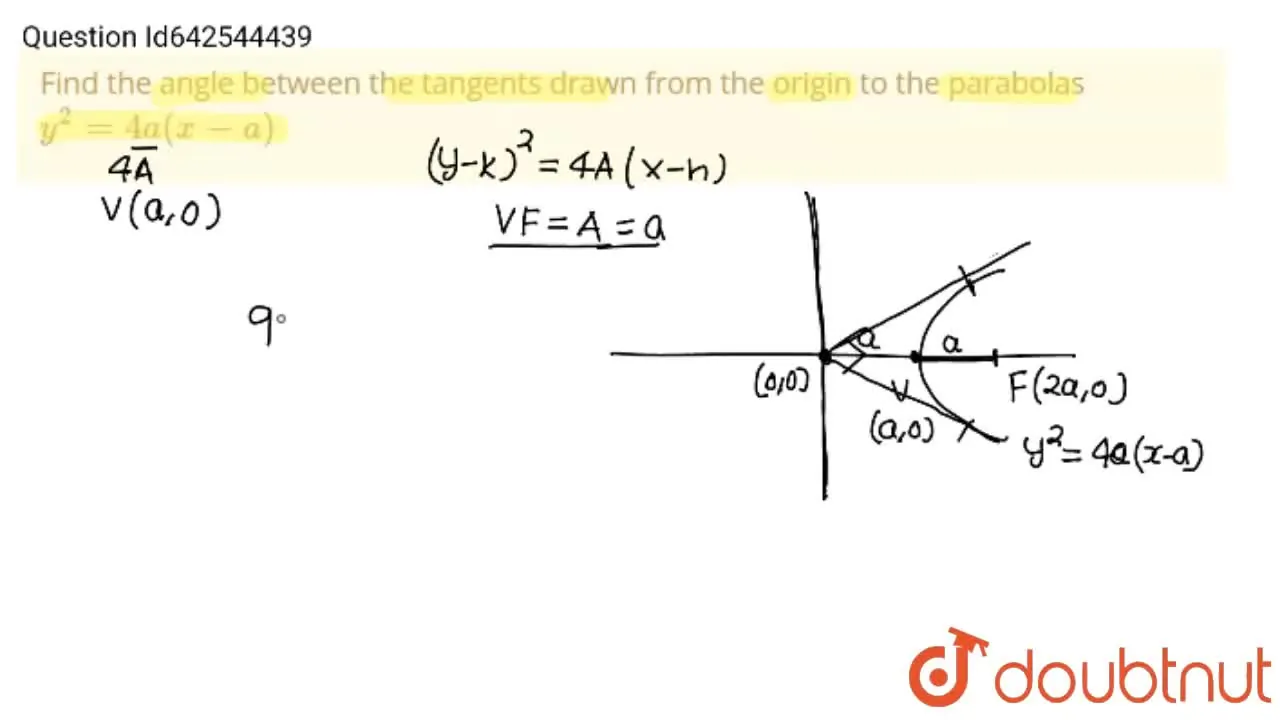
Find the angle between the tangents drawn from the origin to the parabolas y2=4a(x−a)
The correct Answer is:90∘
The origin (0,0) lies on the directrix of the given parabola which is y=0. Then, the angle between the tangents is 90∘.
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - Concept Applications Exercise 5.68videos
PARABOLA
- BOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - Concept Applications Exercise 5.79videos
PARABOLA
- BOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - Concept Applications Exercise 5.413videos
PARABOLA
- BOOK - CENGAGE ENGLISHCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Numberical Value Type5videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Comprehension8videos
PERMUTATION AND COMBINATION
Similar Questions
Find the angle between the tangents drawn from (1, 3) to the parabola y2=4x.
View SolutionFind the angle between two tangents drawn from the point ( 1,4) to the parabola y2=12x
View SolutionThe angle between the tangents drawn from the point (4, 1) to the parabola x2=4y is
View SolutionThe angle between the tangents drawn from the point (1,4) to the parabola y2=4x is (A) π6 (B) π4 (C) π3 (D) π2
View SolutionFind the angle between tangents drawn from P(1,4) to the parabola y2=4x
View SolutionFind the angle between tangents drawn from P(2, 3) to the parabola y2=4x
View SolutionFind angle between tangents drawn from origin to parabola y2=4a(x−a)
View SolutionThe angle between the tangents drawn from the point (2, 6) to the parabola y2−4y−4x+8=0 is
View SolutionThe angle between the tangents drawn form the point (3, 4) to the parabola y2−2y+4x=0, is
View SolutionThe angle between the tangents drawn from the origin to the circle x2+y2+4x−6y+4=0 is
View Solution