एक घन के किन्ही दो विकर्णों के मध्य कोण ज्ञात कीजिए ।
माना ABCDEFG एक घन है।
तथा A≡A(a,0,0),B≡B(a,0,a)
C≡C(0,0,a),D≡D(0,a,a)
E≡E(a,a,a),F≡F(a,a,0)
G≡G(0,a,0)
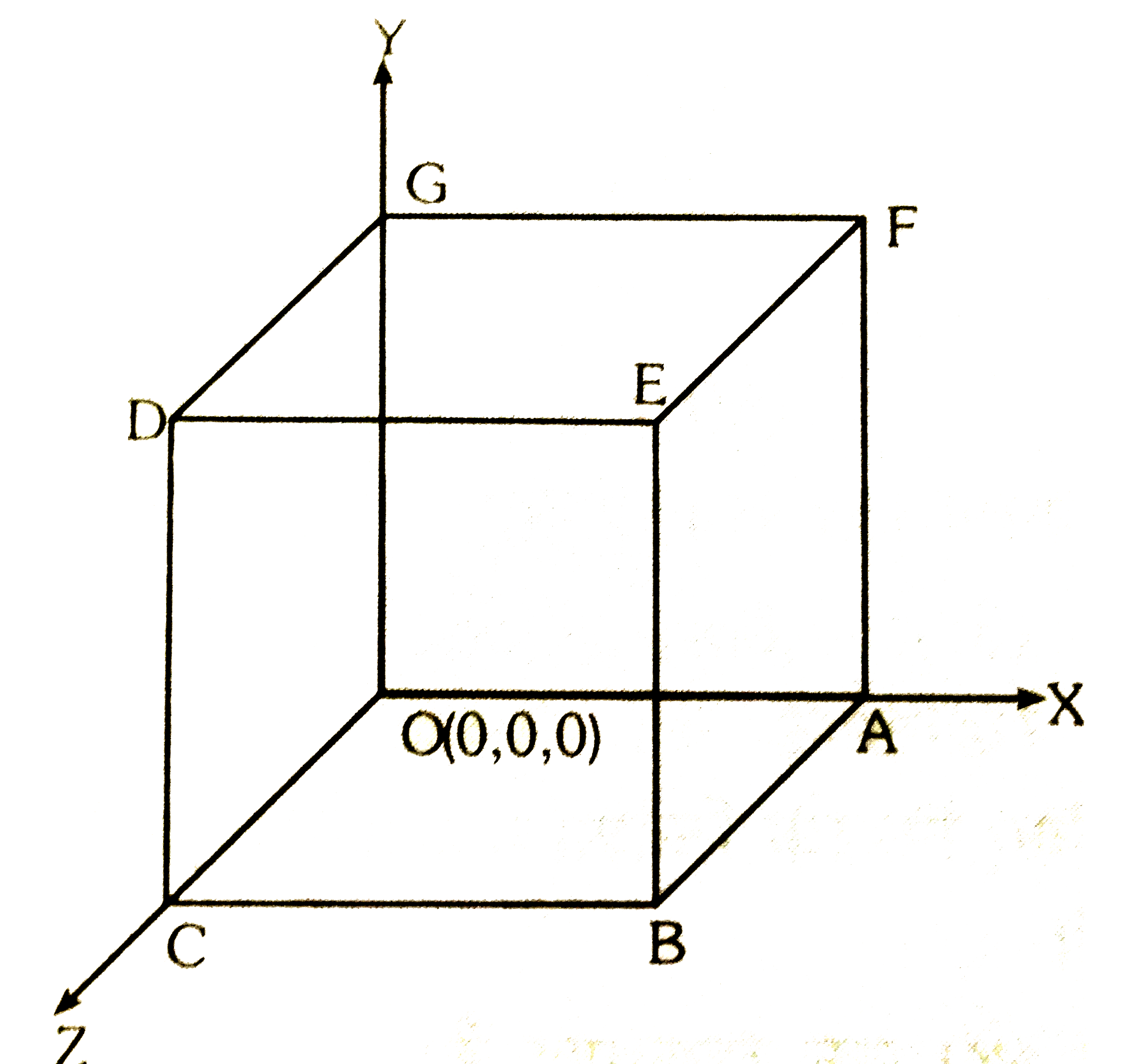
हम जानते ही की घन की चार विकर्ण होते है।
अथार्त OE,AD,CF तथा DB विकर्ण है तब OE के दिक् अनुपात a,a,a या 1,1,1
∴ इनकी दिक् कोज्यायें 1√3,1√3,1√3
अब AD के दिक् अनुपात −a,a,a या −1,1,1 है।
इसकी दिक् कोज्यायें −1√3,−1√3,−1√3 है।
इसी प्रकार CF तथा GB की दिक् कोज्यायें क्रमशः है
1√3,1√3,−1√3 तथा 1√3,−1√3,1√3
∴ किन्ही दो विकर्ण OE तथा Ad के मध्य न्यूनकोण θ
θ=cos−1[(1√3)(−1√3)+(1√3)(1√3)+(1√3)(1√3)]
⇒θcos−113
Related Playlists
- BOOK - BALAJI PUBLICATIONCHAPTER - त्रिविमीय ज्यामिति : सरल रेखायें एवं समतल EXERCISE - अभ्यास प्रश्न 22.116videos
त्रिविमीय ज्यामिति : सरल रेखायें एवं समतल
- BOOK - BALAJI PUBLICATIONCHAPTER - त्रिविमीय ज्यामिति : सरल रेखायें एवं समतल EXERCISE - अभ्यास प्रश्न 22.221videos
त्रिविमीय ज्यामिति : सरल रेखायें एवं समतल
- BOOK - BALAJI PUBLICATIONCHAPTER - खण्डश: समाकलन EXERCISE - स्वमूल्यांकन परीक्षण28videos
खण्डश: समाकलन
- BOOK - BALAJI PUBLICATIONCHAPTER - द्विआधारी संक्रियाएँ EXERCISE - स्वमूल्यांकन परीक्षण11videos
द्विआधारी संक्रियाएँ
Similar Questions
निम्नलिखित सदिशों की दिक् कोज्याये ज्ञात कीजिए-
(i) 2ˆi+2ˆj−ˆk
(ii)6ˆi−2ˆj−3ˆk06:31View Solutionउस रेखा का समीकाण ज्ञात कीजिए जो बिन्दु (1,2,3) से होकर जाती है तथा रेखा −x−21=y+37=2z−63 के समान्तर है ।
06:40View Solutionx sin x का समाकलन कीजिए-
02:17View Solutionसिद्ध कीजिए की a∗b=a+2b द्वारा प्रदर्शित ⋅:R×R→R क्रमविनिमेय नहीं है|
07:40View Solutionएक आयत की भुजाएँ x=2,x=−4,y=3 और y=−5 है। इसके विकर्णों के समीकरण ज्ञात कीजिए ।
02:14View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
02:26View Solutionनिम्न समतलों के मध्य कोण ज्ञात कीजिए:
¯r⋅(i+j+2k)=5तथा¯r⋅(2i−j+2k)=602:14View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
02:08View Solutionसमतलो ¯r.(2i−3j+4k)=1 और ¯r(−i+j)=4 के मध्य कोण ज्ञात कीजिए।
04:18View Solutionनिम्न समतलो के मध्य कोण ज्ञात कीजिए -
x+y+2z=9 और 2x−y+z=1550:39View Solutionनिम्न समतलो के मध्य कोण ज्ञात कीजिए -
2x−y+z=4 और x+Y+2z=350:23View Solutionनिम्न समतलो के मध्य कोण ज्ञात कीजिए -
x+y−2z=3 और 2x−2y+z=540:50View Solutionउन रेखाओं के मध्य कोण ज्ञात कीजिए जिसमें एक दिक् - अनुपात 2, 1, 2 है और रेखा बिंदुओं (1, 4, 3) तथा (2, 12, 7) से जाती है ।
52:52View Solutionदो रेखाओ के मध्य कोण
01:24:42View Solutionदो समतलो के मध्य कोण
01:29:56View Solutionदो रेखाओ के मध्य कोण
03:00View Solution


