Find the altitude of an equilateral triangle of side 8 cm.
A
5√3
B
3√3
C
4√3
D
2√3
Video Solution
Text Solution
The correct Answer is:C
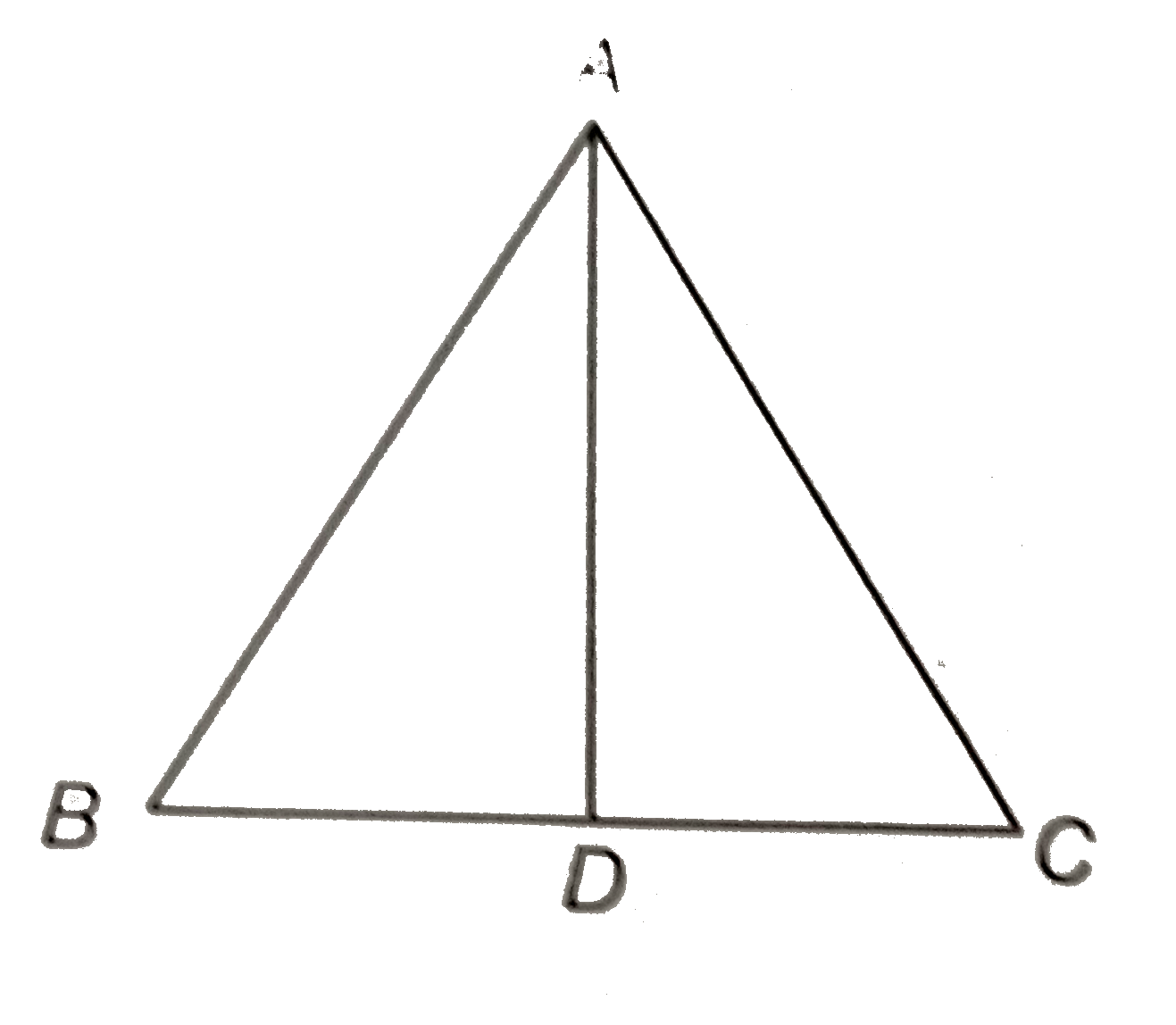
Let ABC be an equilateral triangle of side 8 cm. i.e, AB=BC=CA=8 cm.
Draw altitude AD which is perpendicular to BC. Then, D is the mid-point of BC.
∴BD=CD=12BC=82=4cm
Now, AB2=AD2+BD2 [by Pythagoras theorem]
⇒(8)2=AF2+(4)2
⇒64=AD2+16
⇒AD2=64−16=48
⇒AD=√48=4√3
Hence, altitude of an equileteral triangle is 4√3 cm
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Find the length of the altitude of an equilateral triangle of side 2a cm.
View SolutionFind the area of an equilateral triangle of side 8 cm .
View SolutionFind the length of the altitude of an equilateral triangle of side 9√3cm.
View SolutionFind the height of an equilateral triangle of side 12 cm
View SolutionFind the length of the altitude of an equilateral triangle with side 6 cm.
View SolutionFind the length of the altitude of an equilateral triangle with side 6 cm.
View SolutionFind the area of an equilateral triangle of side 12 cm.
View SolutionFind the area of an equilateral triangle of side 6 cm.
View SolutionFind the area of an equilateral triangle of side 6 cm.
View SolutionWhat is the length of an altitude of an equilateral triangle of side 8cm?
View Solution


