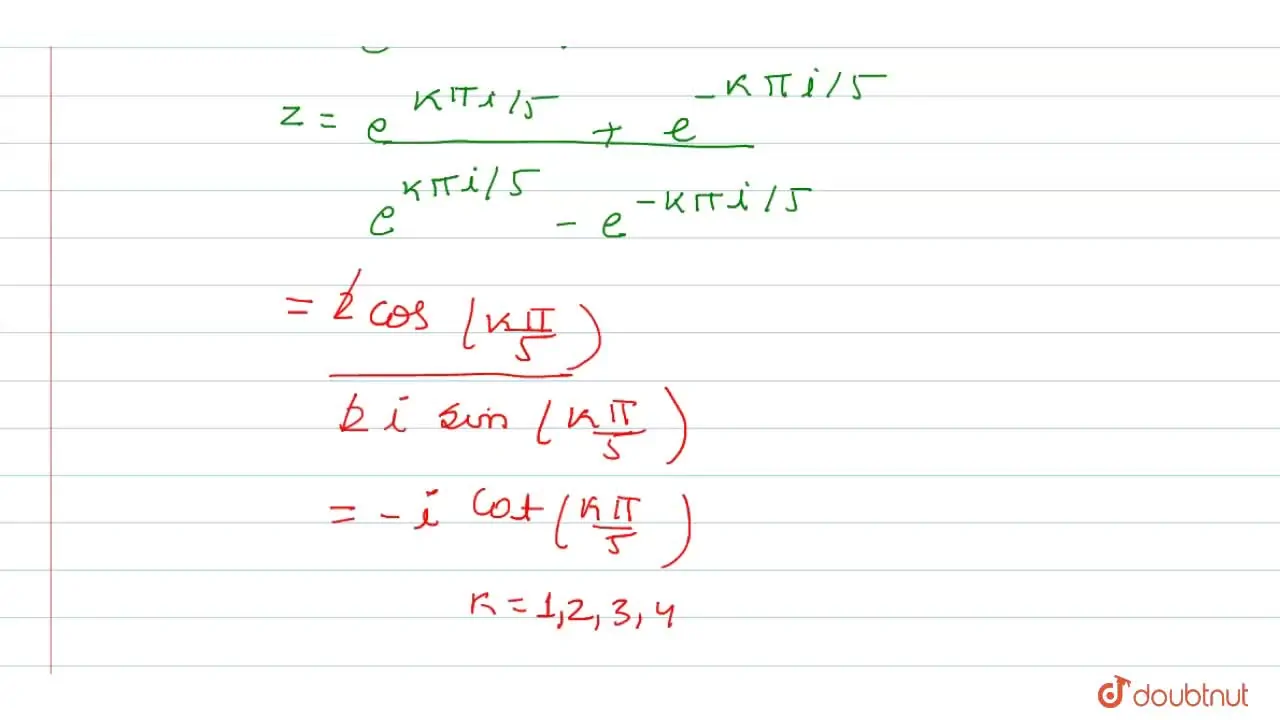Find roots of the equation (z+1)5=(z−1)5.
For z≠1, given equation can be written as (z+1z−1)5=1.
∴ z+1z−1=e2kπi5,where k=1,2,3,4
⇒ z=e2kπi/5+1e2kπi/5−1=ekπi/5+e−kπi/5ekπi/5−e−kπi/5
=2cos(kπ/5)2isin(kπ/5)
=−icot(kπ5),k=1,2,3,4
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - SLOVED EXAMPLES15videos
COMPLEX NUMBERS
- BOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE3.14videos
COMPLEX NUMBERS
- BOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - Comprehension11videos
COMPLEX NUMBERS
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
- BOOK - CENGAGE ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - All Questions101videos
CONIC SECTIONS
Similar Questions
Find the number of roots of the equation z15=1 satisfying |argz|<π/2.
View SolutionIf z1 and z2 are the complex roots of the equation (x−3)3+1=0, then z1+z2 equal to
View SolutionProve that quadrilateral formed by the complex numbers which are roots of the equation z4−z3+2z2−z+1=0 is an equailateral trapezium.
View SolutionSum of common roots of the equations z3+2z2+2z+1=0 and z1985+z100+1=0 is
View SolutionRoots of the equation are (z+1)5=(z−1)5 are
(a) ±itan(π5),±itan(2π5)
(b)±icot(π5),±icot(2π5)
(c)±icot(π5),±itan(2π5)
(d)none of theseView SolutionCommon roots of the equation z3+2z2+2z+1=0 and z2020+z2018+1=0, are
View SolutionIf z1,z2,z3andz4 are the roots of the equation z4=1, the value of4∑i=1z3iis
View SolutionFor a complex number z, the product of the real parts of the roots of the equation z2−z=5−5i is (where, i=√−1)
View SolutionIf z1,z2,z3 are any three roots of the equation z6=(z+1)6, then arg(z1−z3z2−z3) can be equal to
View Solutionlet z1,z2,z3 and z4 be the roots of the equation z4+z3+2=0 , then the value of 4∏r=1(2zr+1) is equal to :
View Solution