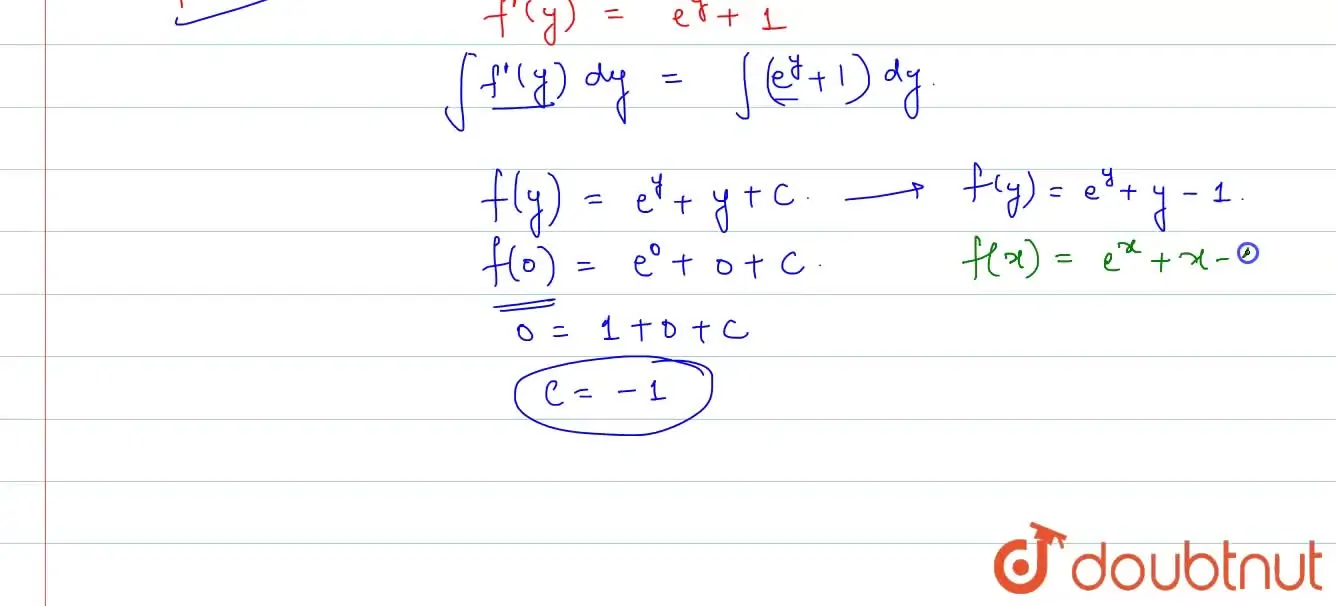Find function f(x) which is differentiable and satisfy the relation f(x+y)=f(x)+f(y)+(ex−1)(ey−1)∀x,y∈R,andf'(0)=2.
We have
f(x+y)=f(x)+f(y)+(ex−1)(ey−1)∀x,∈R ...(1)
Differentiating w.r.t. x, keeping y as constant, we get
f(x+y)=f'(x)+ex(ey−1)
Putting x=0
f'(y)=f'(0)+ey−1
∴ f'(y)=ey+1 (asf'(0)=2)
∴ f(y)=ey+y+c
Putting x = y = 0 in (1), we get
f(0)=f(0)+f(0)+0
∴ f(0)=0
In (2), putting y=0, we get
0=1 +0+c
⇒ c=−1
∴ f(x)=ex+x−1
Related Playlists
- BOOK - CENGAGECHAPTER - DIFFERENTIATIONEXERCISE - Exercise 3.17videos
DIFFERENTIATION
- BOOK - CENGAGECHAPTER - DIFFERENTIATIONEXERCISE - Exercise 3.238videos
DIFFERENTIATION
- BOOK - CENGAGECHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Question Bank25videos
DIFFERENTIAL EQUATIONS
- BOOK - CENGAGECHAPTER - DOT PRODUCTEXERCISE - DPP 2.115videos
DOT PRODUCT
Similar Questions
Let f:R−{0}→R be a function which is differentiable in its domain and satisfying the equation f(x+y)=f(x)+f(y)+x+yxy−1x+y, also f'(1)=2. Then find the function.
View SolutionA function f(x) satisfies the relation f(x+y)=f(x)+f(y)+xy(x+y),∀x,y∈R. If f'(0) = - 1, then
View SolutionIf f satisfies the relation f(x+y)+f(x−y)=2f(x)f(y)∀x,y∈Kandf(0)≠0; then f(10)−f(−10)−
View SolutionA continuous function f(x)onR→ satisfies the relation f(x)+f(2x+y)+5xy=f(3x−y)+2x2+1for∀x,y∈R.Thenf∈df(x).
View SolutionLet f(x) be a differentiable function satisfying f(y)f(xy)=f(x) ∀, x,y∈R, y≠0 and f(1)≠0, f'(1)=3 then
View SolutionIf f is a differentiable function satisfying 2f(x)=f(xy)+f(xy),∀x,y∈R+,f(1)=0 and f'(1)=1ln6, then f(7776)=
View SolutionIf f is a differentiable function such that f(xy)=f(x)+f(y):x,y∈R, then f(e)+f(1e) is
View SolutionIf a function satisfies (x−y)f(x+y)−(x+y)f(x−y)=2(x2y−y3)∀x,y∈Randf(1)=2, then
View SolutionLet f:R→R be a differentiable function with f(0)=1 and satisfying the equation f(x+y)=f(x)f′(y)+f′(x)f(y) for all x, y∈R . Then, the value of (log)e(f(4)) is _______
View SolutionIf f is a real valued differentiable function satisfying |f(x)−f(y)|≤(x−y)2,x,y∈R and f(0)=0, then f(1) equals :
View Solution