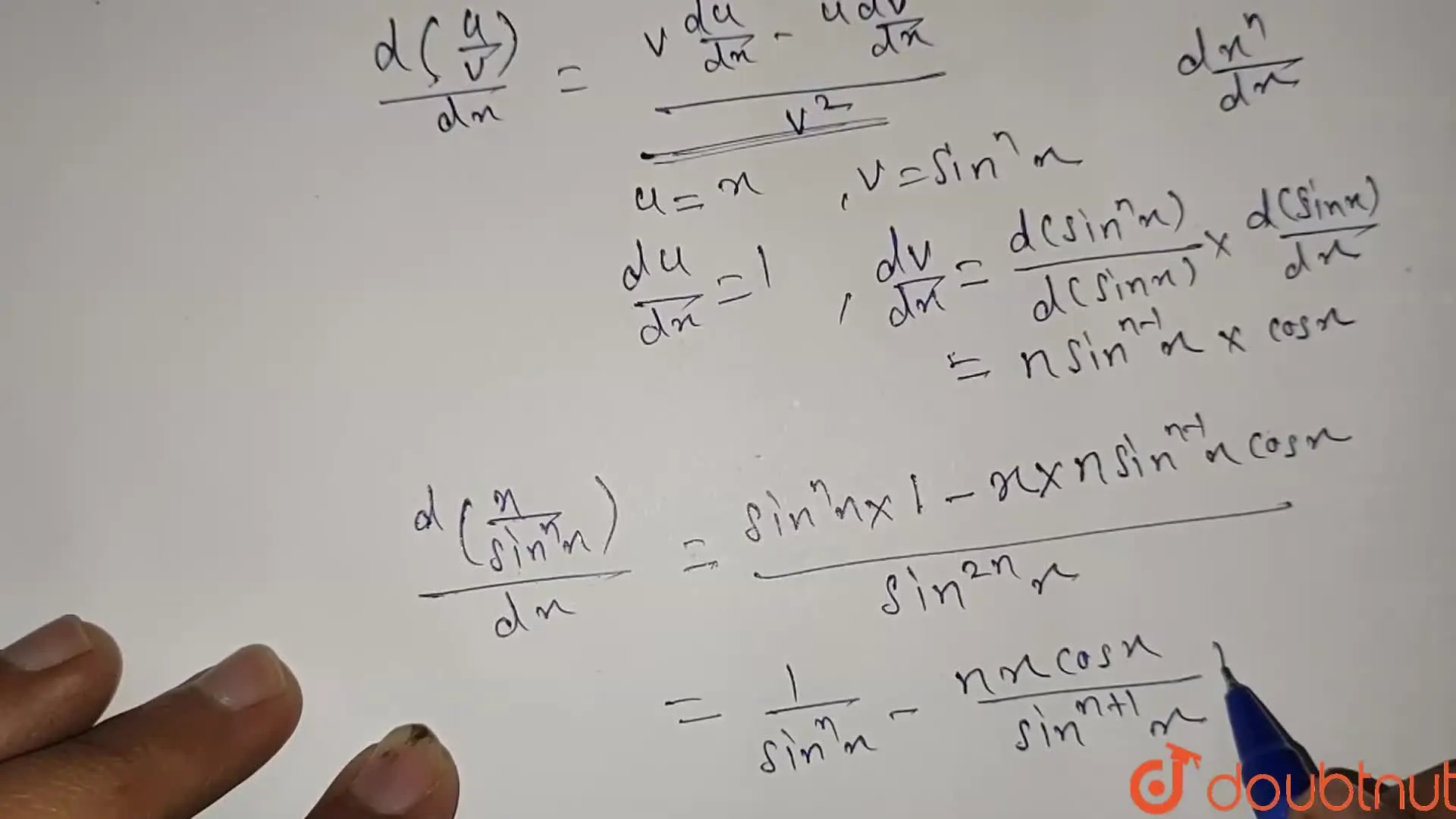Find derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): xsinnx
Given,
f(x)=xsinnx
Now, As we know the derivative of any function
d(y1y2)dx=y2d(dy1dx)−y1(dy2dx)y22
⇒d(xsinnx)dx=sinnxd(dxdx)−x(dsinnxdx)sin2nx
Further solving this we will get
d(xsinnx)dx=sinx−nxcosxsinn+1x
Related Playlists
- BOOK - NCERT ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - EXERCISE 13.211videos
LIMITS AND DERIVATIVES
- BOOK - NCERT ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - EXERCISE 13.38videos
LIMITS AND DERIVATIVES
- BOOK - NCERT ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - SOLVED EXAMPLES25videos
LIMITS AND DERIVATIVES
- BOOK - NCERT ENGLISHCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - EXERCISE 12.14videos
INTRODUCTION TO THREE DIMENSIONAL GEOMETRY
- BOOK - NCERT ENGLISHCHAPTER - LINEAR INEQUALITIESEXERCISE - EXERCISE 6.210videos
LINEAR INEQUALITIES
Similar Questions
Find derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): (x+a)
View SolutionFind derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): sinnx
View SolutionFind derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): (ax+b)n
View SolutionFind derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): cosx1+sinx
View SolutionFind derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): ax+bcx+d
View SolutionFind derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): 1ax2+bx+c
View SolutionFind derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): sin(x+a)cosx
View SolutionFind derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): sin (x + a)
View SolutionFind derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): 4x+5sinx3x+7cosx
View SolutionFind derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): (ax2+sinx)(p+qcosx)
View Solution