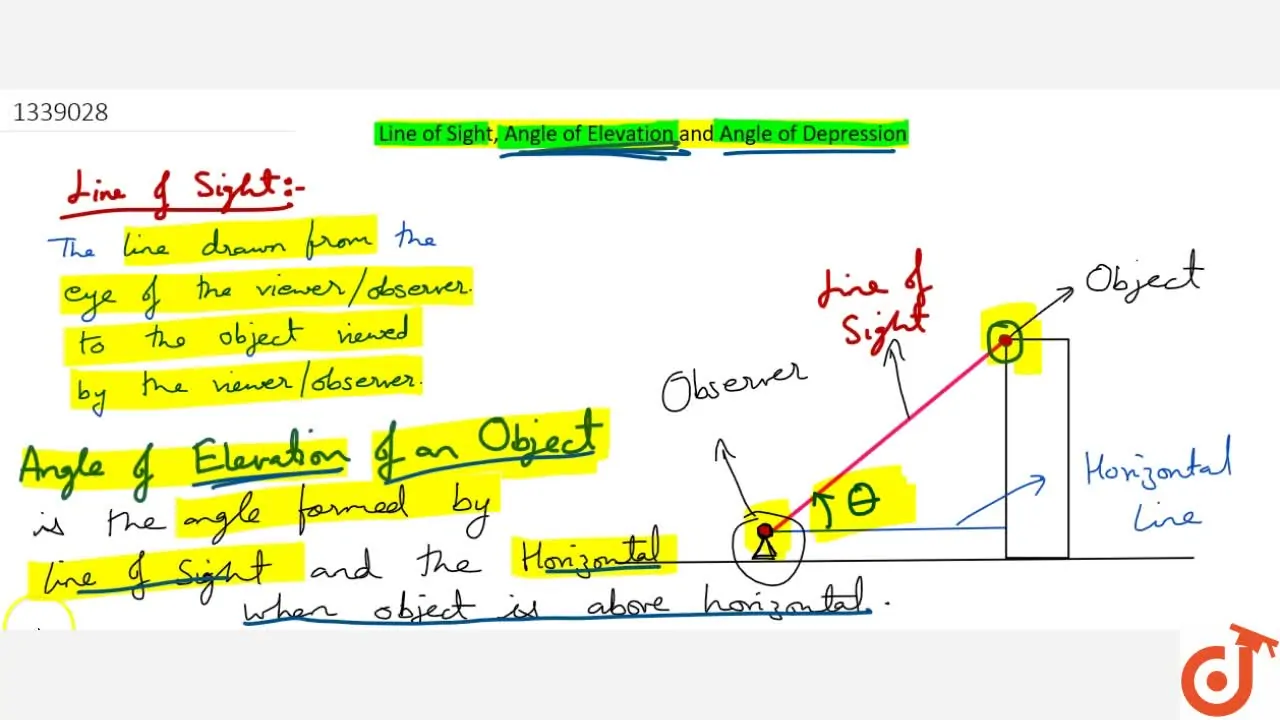
Explain the angle of elevation & depression with the help of diagram.
Step by step video & image solution for Explain the angle of elevation & depression with the help of diagram. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Similar Questions
Angle of Elevation and Depression
View SolutionExplain the meaning of deflationary gap with the help of a diagram.
View SolutionExplain biofuel production with the help of a diagram
View SolutionExplain the functioning of lac operon system with the help of a diagram.
View SolutionExplain the structure of a nephron with the help of a labelled diagram.
View SolutionA boy is standing at the top of the tower and another boy is at the ground at some distance from the foot of the tower, then the angle of elevation and depression between the boys when both look at each other will be (a) Equal (b) Angle of elevation will be greater (c) Cannot be predicted for relation (d) Angle of depression will be greater
View SolutionExplain the structure of neuron with the help of a labelled diagram.
View SolutionWhat is the phenomenon of electrolysis? Explain with the help of diagram.
View SolutionWhat is the cause of friction ? Explain with the help of labelled diagram.
View SolutionProblems based on finding the angle of elevation/depression Ex- If the height of the pole is 2√3 meters and the length of the shadow is 2 meters, find the angle of the elevation of the sun
View Solution