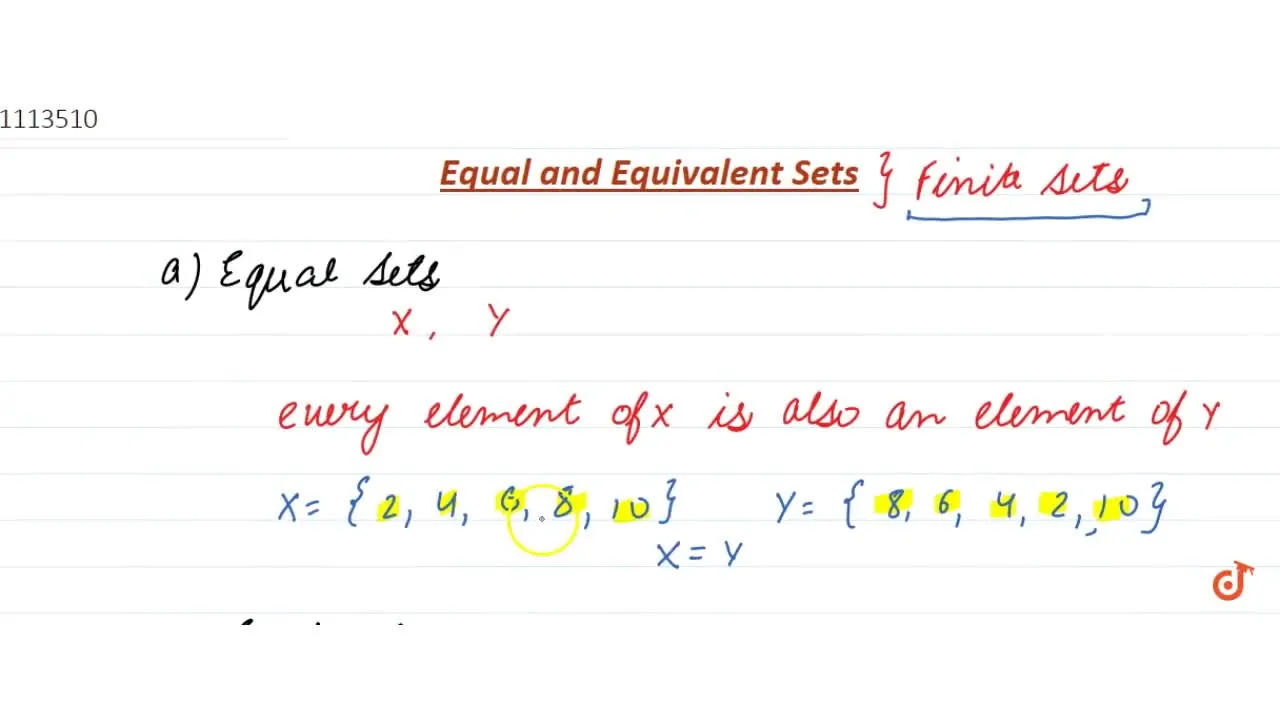Explain Equivalent sets and equal sets with examples
Step by step video & image solution for Explain Equivalent sets and equal sets with examples by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
Explain Empty Sets ; Finite sets and Infinite sets with examples..
View SolutionExplain Intersection of sets with diagram & examples ?
View Solution. If A is a set of vowels and B is a set of first five natural numbers then
A and B are comparable sets
A and B are equal sets
Equivalent sets
None of theseView SolutionIf A is a set of vowels and B is a set of first five natural numbers then
A and B are comparable sets
A and B are equal sets
Equivalent sets
none of theseView SolutionWhat is Universal Sets ? (Explain with examples)
View SolutionWhat is Power Sets ? (Explain with examples)
View SolutionIs inclusion of a subset in another, in the context of a universal set, an equivalence relation in the class of subsets of the sets? Justify your answer.
View SolutionExplain Union of sets with diagram & examples ?
View SolutionWhat is Cartesian product of 2 sets ? (explain with example)
View SolutionWhat is Cartesian product of 3 sets ?(explain with example)
View Solution