Examine which is greater : sin x tan x or x2, Hence evaluate limh→0[sinxtanxx2], Where x∈(0,π2)
Video Solution
Text Solution
Let f(x)sinxtanx=x2
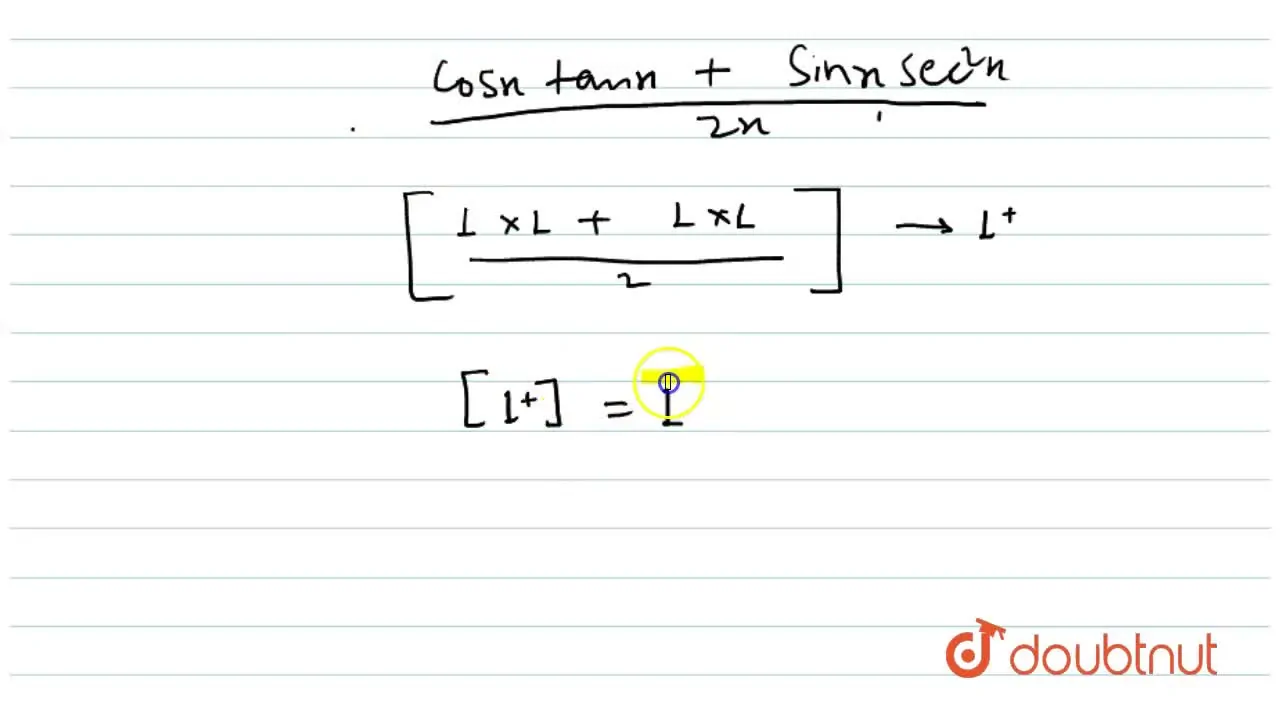
f(x)=cosx,tanx+sinx.sec2−2x⇒f(x)=sinx+sinxsec2−2x
⇒f(x)=cosx+cosxsec2+2sec2sinxtanx−2
⇒f(x)=(cosx+secx−2)+2sec2xsinxtanx
Now cosx+secx−2=(√cosx−√secx)2 and 2 sec2xtanx. sin x > 0 because x∈(0,π2)
⇒f(x)>0⇒f(x) is M.I.
Hence f(x)>f(0)
⇒f(x)>0⇒f(x) is M.I⇒f(x)>0
⇒sinxtanx−x2>0
Hence sin x tan x >x2⇒sinxtanxx2>1⇒limh→0[sinxtanxx2]=1.
|
Updated on:21/07/2023
Related Playlists
- BOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Self Practice Problems34videos
APPLICATION OF DERIVATIVES
- BOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise -1A5videos
APPLICATION OF DERIVATIVES
- BOOK - RESONANCECHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-II: Previously Asked Question of RMO)8videos
COMBINATORICS
Similar Questions
Evaluate: limx→0sinxtanx
View SolutionEvaluate limx→0sin24xx2
View SolutionEvaluate limx→0tanx−sinxx3
View SolutionEvaluate: limx→0tanx−sinxx3
View SolutionEvaluate limx→02sinx−sin(2x)x3
View SolutionEvaluate limh→0√x+h−√xh
View SolutionEvaluate limx→0tan3x−2x3x−sin2x
View Solutionlimx→0xtan3xsin2x is
View SolutionEvaluate : Limx→0sin4xsin2x
View SolutionEvaluate limx→0sin2x+tan3x4x−sin5x
View Solution