Evaluate limx→3x7−2187x−81
Video Solution
Text Solution
We have, limx→3x7−2187x4−81=limx→3(x7)−(3)7(x4)−(3)4
=limx→3x7−x7x4−34x−3x−3=limx→3x7−37x−3x4−34x−3
=limx→3x7−37x−3/limx→3x4−34x−3⎡⎣∵limx→af(x)g(x)=limx→af(x)limx→ag(x)⎤⎦
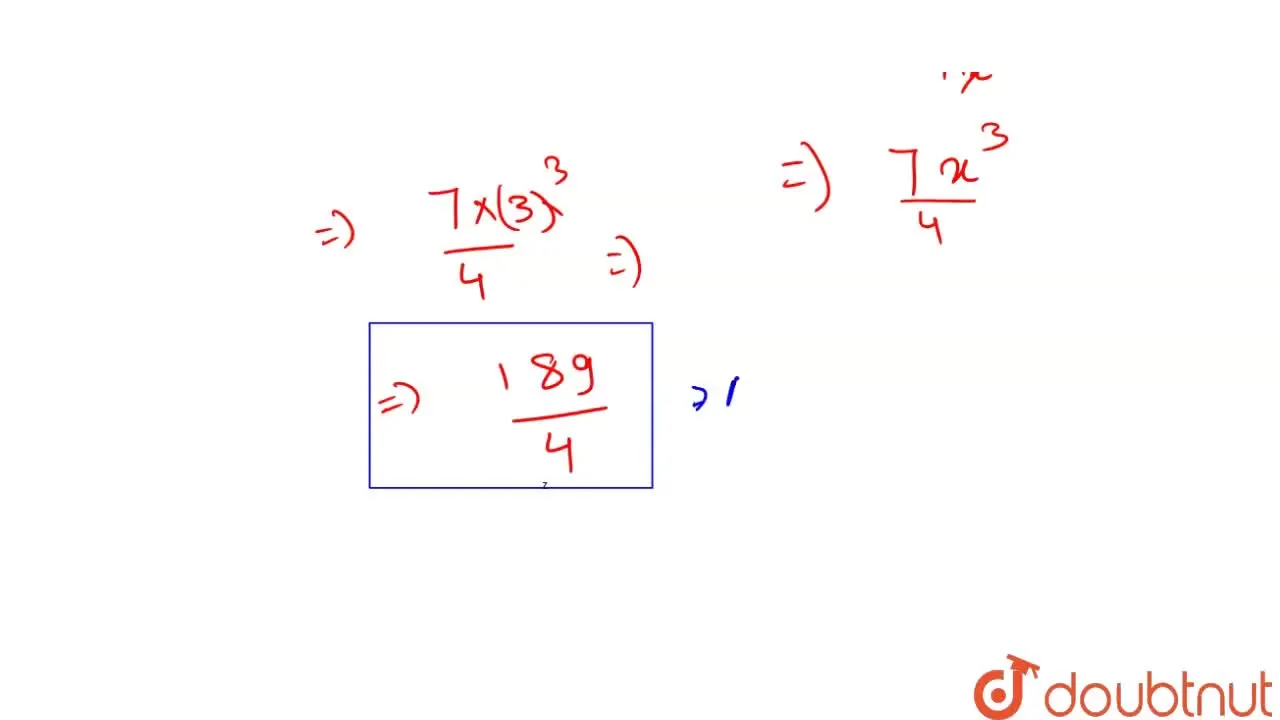
=(3)7−1/4(3)4−1=7.36/4.33=7433=1894
|
Updated on:21/07/2023
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - LIMITS AND DERIVATIVES EXERCISE - Try yourself64videos
LIMITS AND DERIVATIVES
- BOOK - AAKASH INSTITUTECHAPTER - LIMITS AND DERIVATIVES EXERCISE - SECTION - A50videos
LIMITS AND DERIVATIVES
- BOOK - AAKASH INSTITUTECHAPTER - LIMITS AND DERIVATIVES EXERCISE - Section - j3videos
LIMITS AND DERIVATIVES
- BOOK - AAKASH INSTITUTECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - ASSIGNMENT (SECTION - J)(ANKASH CHALLENGERS QUESTIONS)4videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - AAKASH INSTITUTECHAPTER - MATHEMATICAL REASONINGEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)15videos
MATHEMATICAL REASONING
Similar Questions
Evaluate limx→1x3−1x−1
View SolutionEvaluate limx→16x3/2−64x−16
View SolutionEvaluate limx→3x2−9x+2
View SolutionEvaluate, limx→2x3−8x2−4
View SolutionEvaluate : limx→3[x(x+1)].
View SolutionEvaluate: limx→3[x3−27x−3].
View SolutionEvaluate limx→4x2−7x+12x2−16
View SolutionEvaluate limx→2√3−x−12−x
View SolutionEvaluatelimx→1x3−1x2−1
View SolutionEvaluate: limx→3x5−243x−3.
View Solution