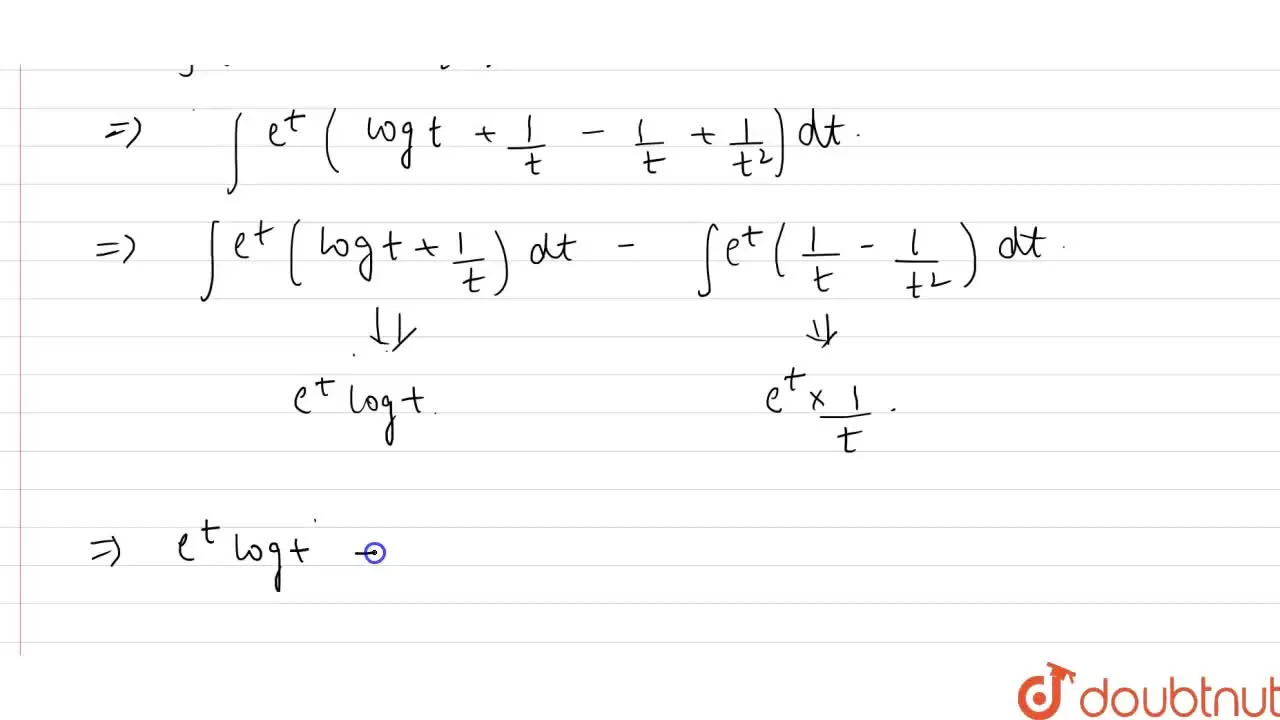Evaluate the following integrals:
∫{log(logx)+1(logx)2}dx
Video Solution
Text Solution
The correct Answer is:x⋅{log(logx)−1logx}+C
Puttint logx=t,x=etanddx=etdt, we get
I=∫{logt+1t2}etdt=∫et{logt+1t−1t+1t2}dt
=∫et(logt+1t)dt−∫et(1t−1t2)dt=etlogt−et⋅1t+C
=x{log(logx)−1logx}+C.
|
Updated on:21/07/2023
Related Playlists
- BOOK - RS AGGARWALCHAPTER - METHODS OF INTEGRATION EXERCISE - Objective Questions Ii56videos
METHODS OF INTEGRATION
- BOOK - RS AGGARWALCHAPTER - METHODS OF INTEGRATION EXERCISE - Exercise 13B34videos
METHODS OF INTEGRATION
- BOOK - RS AGGARWALCHAPTER - MATRICESEXERCISE - Exercise 5F21videos
MATRICES
- BOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Exercise 29 B2videos
PROBABILITY
Similar Questions
Evaluate the following integrals:
∫{1logx−1(log)2}dxView SolutionEvaluate the following integrals:
∫log(logx)xdxView SolutionEvaluate the following integrals:
∫e−logxdxView SolutionEvaluate the following integrals:
∫logxxndxView SolutionEvaluate the following integrals:
∫logx(1+logx)2dxView SolutionEvaluate the following integral: ∫∞0logx1+x2dx
View SolutionEvaluate :
∫{log(logx)+1(logx)2}dxView SolutionEvaluate the following integral: ∫31cos(logx)xdx
View SolutionEvaluate the following integrals:
∫ex(logx+1x2)dxView Solution∫{1(logx)−1(logx)2}dx=?
View Solution