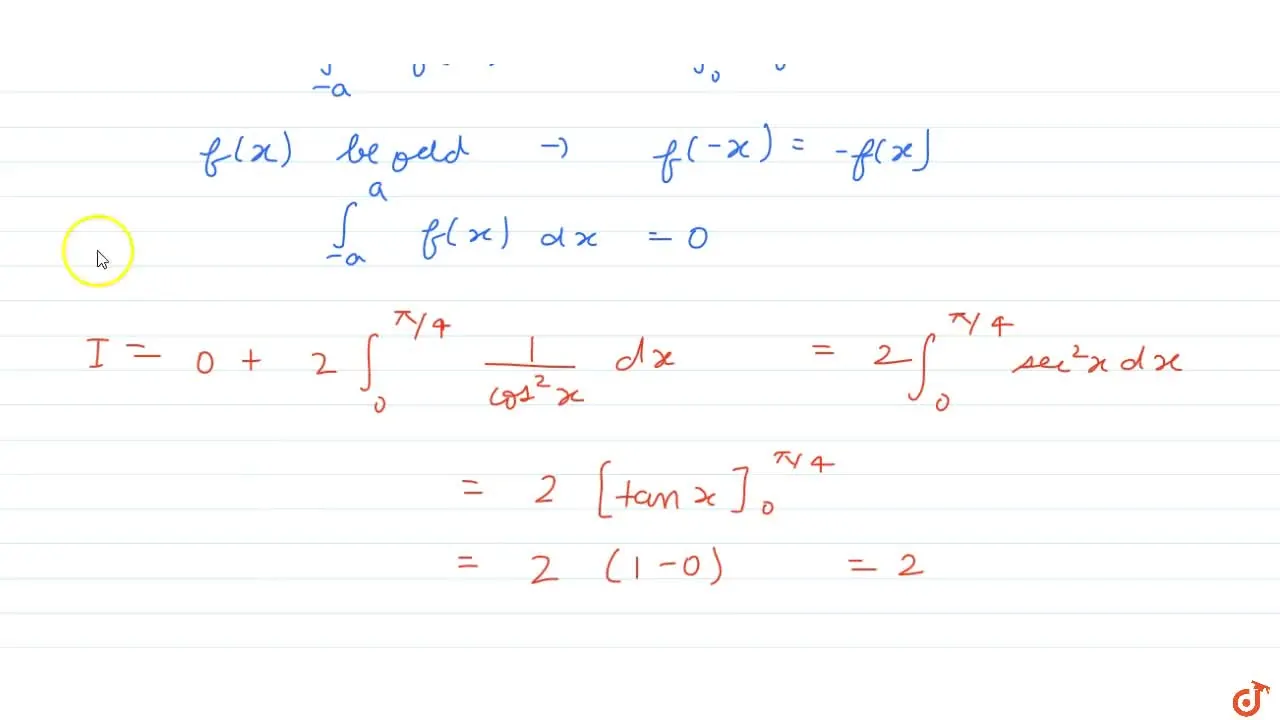Evaluate of each of the following integrals (1-15): ∫π/4−π/4x11−3x9+5x7−x5+1cos2xdx
Video Solution
Text Solution
LetI=∫x4−π4x11−3x9+5x7−x5+1cos2xdx
=∫π4−π4x11−3x9+5x7−x5cos2xdx+∫π4−π41cos2xdx
=∫π4−π4x11−3x9+5x7−x5cos2xdx+∫x4−x4sec2xdx
=I1+I2
Now,
Consider
f(x)=x11−3x9+5x7−x5cos2x
∴f(−x)=(−x)11−3(−x)9+5(−x)7−(−x)5cos2(−x)
=−x11+3x9−5x7+x5cos2x
=−x11−3x9+5x7−x5cos2x=−f(x)
Let
g(x)=sec2x
∴g(−x)=sec2(−x)=sec2x=g(x)
⇒I2=∫x4−π4sec2xdx
=2∫x40sec2xdx....................[∫a−af(x)dx=2∫a0f(x)dx,{if}f(−x)=f(x)=0,{if}f(−x)=−f(x)].
=2×.tanx∣∣∣π40
=2(tanπ4−tan0)
=2×(1−0)
=2
∴I=I1+I2=0+2=2
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Evaluate of each of the following integrals (1-15): ∫π/4−π/4x11−3x9+5x7−x5+1cos2xdx
View SolutionEvaluate of each of the following integral: ∫π/4−π/4tan2x1+exdx
View SolutionEvaluate of each of the following integral: ∫π/3−π/311+exdx
View SolutionEvaluate of each of the following integral: ∫π/2−π/2cos2x1+exdx
View SolutionEvaluate of each of the following integrals (1-15): ∫2π0log(secx+tanx)dx
View SolutionEvaluate each of the following integral: ∫π/2−π/2x cos2x dx
View SolutionEvaluate each of the following integral: ∫π/2−π/2cos2x dx
View SolutionEvaluate each of the following integral: ∫π/2eex(sinx−cosx)dx
View Solution∫3π/4π/4dx1+cosx=
View Solution∫π/2π/4dx(1−cos2x)
View Solution