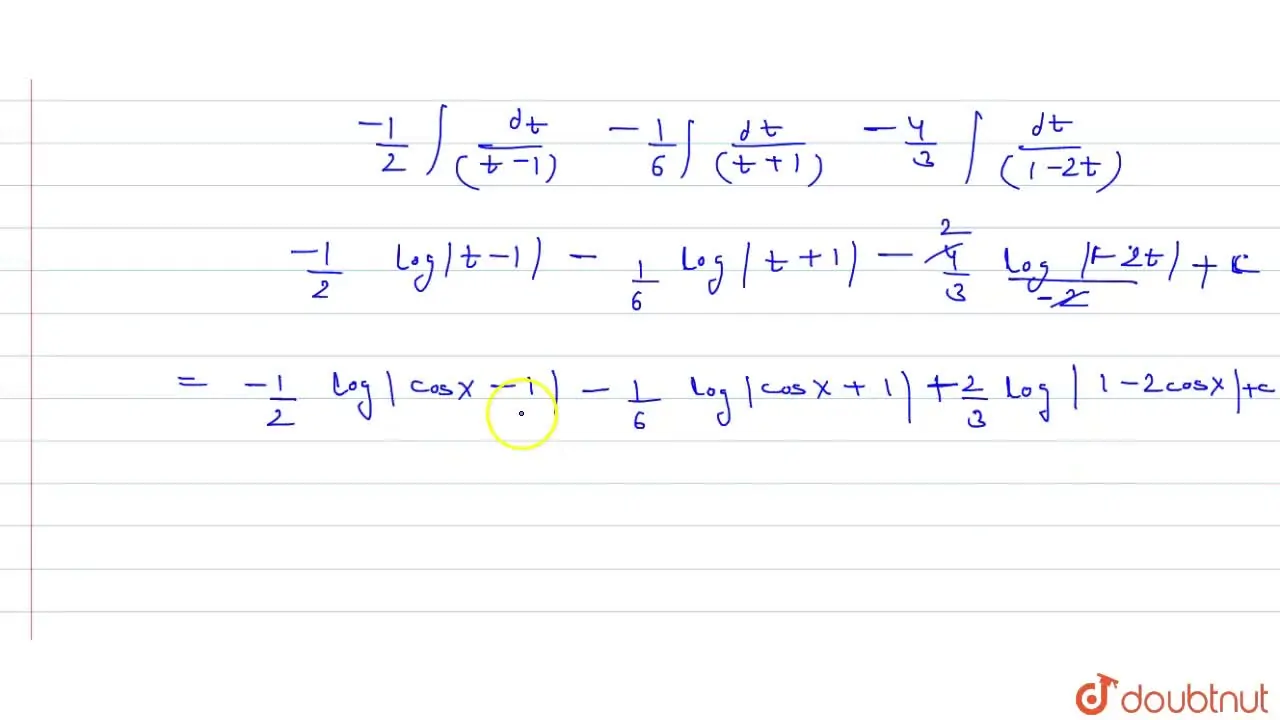Evaluate ∫dx(sinx−sin2x).
Video Solution
Text Solution
∫dx(sinx−sin2x)=∫dx(sins−2sinxcosx)
=∫dxsinx(1−2cosx)=∫sinxsin2x(1−2cosx)dx
∫jsinx(1−cos2x)(1−2cosx)dx
=−∫dt(1−t2)(1−2t),where cos x=t
=∫dt(t−1)(t+1)(1−2t).
Let1(t−1)(t+1)(1−2t)=A(t−1)+B(t+1)+C(1−2t).
then,1≡A(t+1)(1−2t)+B(t−1)(1−2t)+C(t−1)(t+1).
Putting t=1 in (i) , we get A=−12
Putting t=−1 in (ii), we get B=−16.
Putting t=12 in (ii), we get C=−43.
∴I=−12∫dt(t−1)−16.∫dt(t+1)−43.∫dt(1−2t)
=−12log|t−1|−16log|t+1|+23.∫−2dt(1−2t)
=−12log|t−1|−16log|t+1|+23log∣1−2t+C
=−12log|cosx−1|−16log|cosx+1|+23log|1−2cosx|+c.
|
Updated on:21/07/2023
Related Playlists
- BOOK - RS AGGARWALCHAPTER - INTEGRATION USING PARTIAL FRACTIONSEXERCISE - Exercise 15A59videos
INTEGRATION USING PARTIAL FRACTIONS
- BOOK - RS AGGARWALCHAPTER - INTEGRATION USING PARTIAL FRACTIONSEXERCISE - Exercise 15B40videos
INTEGRATION USING PARTIAL FRACTIONS
- BOOK - RS AGGARWALCHAPTER - INDEFINITE INTEGRAL EXERCISE - Objective Questions41videos
INDEFINITE INTEGRAL
- BOOK - RS AGGARWALCHAPTER - INVERSE TRIGNOMETRIC FUNCTIONS EXERCISE - Objective Questons57videos
INVERSE TRIGNOMETRIC FUNCTIONS
Similar Questions
Evaluate: ∫1sinx−sin2xdx
View SolutionEvaluate: ∫1sinx+sin2x dx
View SolutionEvaluate : ∫sinxsin2xdx
View SolutionEvaluate ∫cosx(sin2x+4sinx+5)dx.
View SolutionEvaluate ∫cosx(1−sinx)(2−sinx)dx.
View SolutionEvaluate: ∫1sin2x+sin2xdx
View SolutionEvaluate: ∫1sin2x+sin2x dx
View SolutionEvaluate: ∫sinx2+sin2xdx
View SolutionEvaluate : ∫sinxsin(x−α)dx.
View SolutionEvaluate: ∫cosxsin2x+4sinx+5 dx
View Solution