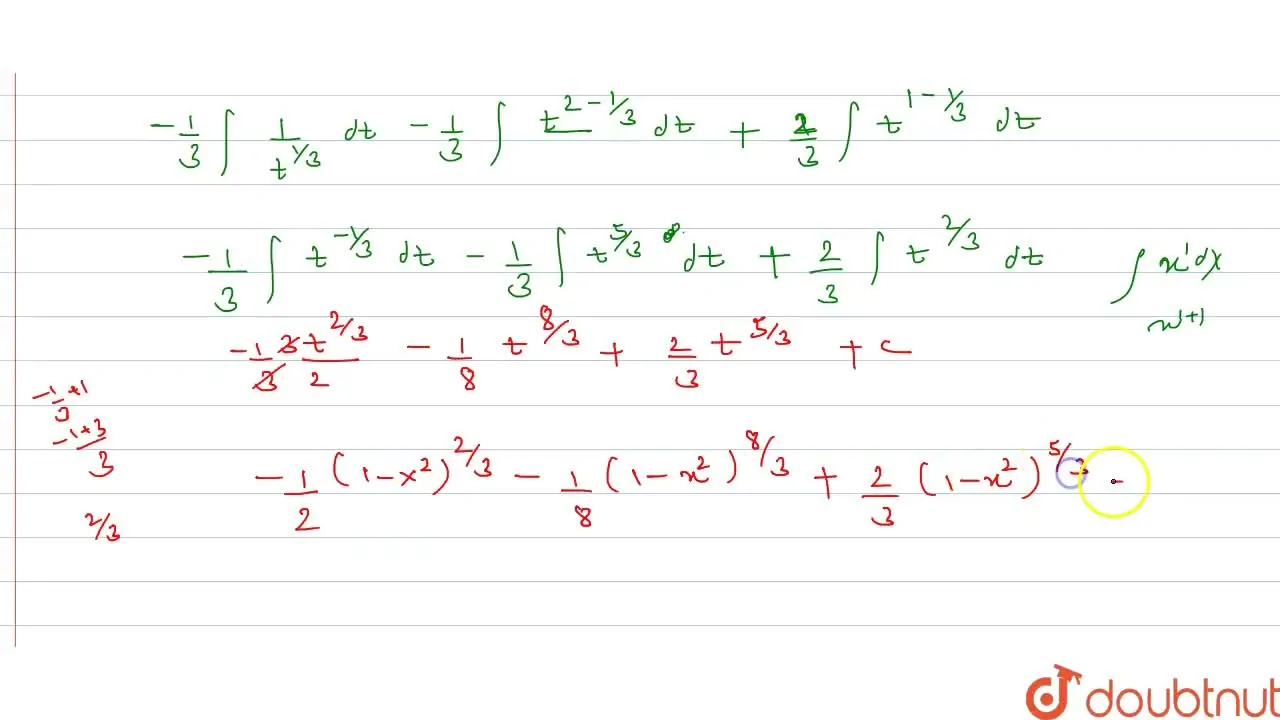Evaluate : (i) ∫3x2(1+x6)dx (ii) ∫x3(x2+1)3dx (iii) x8(1−x3)1/3dx
Video Solution
Text Solution
(i) Put x3=t so that 3x2dx=dt.
∴∫3x2(1+x6)dx=∫dt(1+t2)=tan−1t+C=tan−1x3+C.
(ii) Put (x2+1) =t so that x2=(t−1)andxdx=12dt.
∴∫x3(x2+1)3dx=∫x2⋅x(x2+1)dx
=12∫(t−1)t3dt=12∫1t2dt−1t3dt
=−12t+14t2+C=−12(x2+1)+14(x2+1)2+C
=−1+2x24(x2+1)2+C.
(iii) Put (1=x3)=t so that x3=(1−t)andx2dx=−13dt.
∴∫x8(1−x3)1/3dx=∫x6⋅x2(1−x3)1/3dx
=−13∫(1−t)2t1/3dt=−13(1+t2−2t)tt/3dt
=−13∫t−1/3dt−13∫t5/3dt+23∫t2/3dt
=−12t2/3−18t8/3+25t5/3+C
=−12(1−x3)2/3−18(1−x3)8/3+25(1−x3)5/3+C.
|
Updated on:21/07/2023
Related Playlists
- BOOK - RS AGGARWALCHAPTER - METHODS OF INTEGRATION EXERCISE - EXERCISE 13A VERY SHORT ANSWER QUESTIONS10videos
METHODS OF INTEGRATION
- BOOK - RS AGGARWALCHAPTER - METHODS OF INTEGRATION EXERCISE - EXERCISE 13A SHORT ANSWER QUESTIONS92videos
METHODS OF INTEGRATION
- BOOK - RS AGGARWALCHAPTER - MATRICESEXERCISE - Exercise 5F21videos
MATRICES
- BOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Exercise 29 B2videos
PROBABILITY
Similar Questions
∫3x2+1(x2−1)3dx
View SolutionEvaluate:
(i) ∫x2+x+53x+2 dx
(ii) ∫2x+3(x−1)2 dxView SolutionEvaluate : (i) ∫2x(2x+1)2dx (ii) ∫(2+3x)(3−2x)dx
View SolutionEvaluate (i) ∫tan3/2xsec2x dx (ii) ∫x3(x2+1)3 dx
View SolutionEvaluate:
(i) ∫x2+3x−1(x+1)2 dx
(ii) ∫2x−1(x−1)2 dxView SolutionEvaluate: ∫x2+x+1(x−1)3dx
View SolutionEvaluate: ∫x2(x−1)3(x+1)dx
View SolutionEvaluate: ∫x2(x−1)3(x+1) dx
View SolutionEvaluate : (i) ∫dx(1+3sin2x)
(ii) ∫dx(3+2cos2x)View SolutionEvaluate : ∫x2+3x−12xdx
View Solution