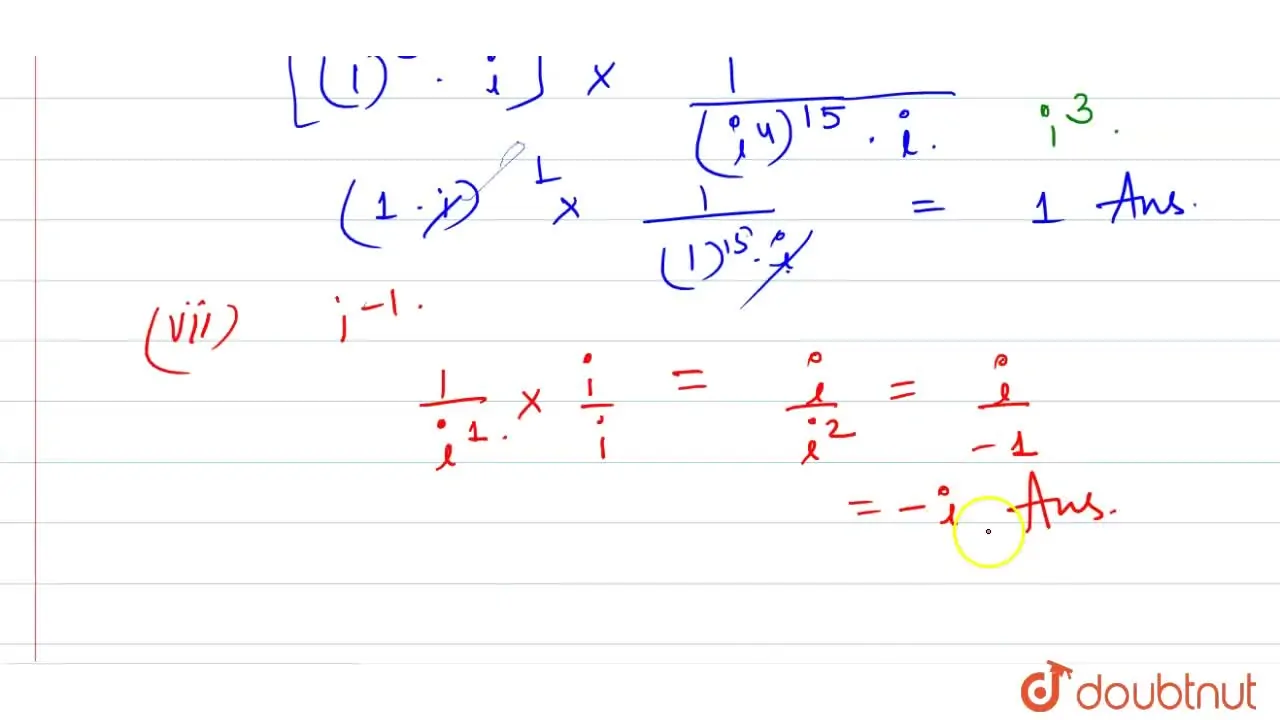Evaluate :
(i)i23 (ii)i998 (iii)i−998 (iv)i−71
(v)(√−1)91 (vi)(i37×i−61) (vii)i−1
We have
(i) i23=i(4×5)+3=(i4)5×i3=i3=−i. [∵i4=1]
(ii) i998=i4×249+2=(i4)249×i2=(1×i2)=i2=−1. [∵i4=1]
(iii) i−998=1i998×i2i2=i2i1000=−11=−1. [∵i1000=(i4)250=1]
(iv) i−71=1i71×ii=ii72=i(i4)18=i1=i. [∵i4=1]
(v) (√−1)91=i91=i4×22+3=(i4)22×i3=1×(−i)=−i. [∵i3=i]
(vi) i37=i4×9+1=(i4)9×i=1×i=i.
i−61=1i61×i3i3=i3i64=−i(i4)16=−i1=−i.
∴ (i37+i−61)=i+(−i)=0.
(vii) i−1=1i=1i×i3i3=−ii4=−i1=−i.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - EXERCISE 5 A15videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
- BOOK - RS AGGARWALCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - EXERCISE 5 B28videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
- BOOK - RS AGGARWALCHAPTER - COMBINATIONSEXERCISE - Exercise 9D18videos
COMBINATIONS
- BOOK - RS AGGARWALCHAPTER - CONDITIONAL IDENTITIES INVOLVING THE ANGLES OF A TRIANGLE EXERCISE - EXERCISE 1612videos
CONDITIONAL IDENTITIES INVOLVING THE ANGLES OF A TRIANGLE
Similar Questions
Evaluate: (i) i−50 (ii) i−9 (iii) i−131
View SolutionEvaluate: (i) i19 (ii) i62 (iii) i373
View SolutionEvaluate the followings :
(i) i23
(ii) i−97View SolutionEvaluate the following
(i) i9
(ii) i342
(iii) i998
(iv) i−63
(v) (i3+1i3)View SolutionEvaluate.
(i) i1998
(ii)i−9999
(iii) (−√−1)4n=3,n ≠ NView SolutionEvaluate :
(i) i135
(ii) i147
(iii) (−√−1)4n+3,n∈N
(iv) √−25+3√−4+2√−9View SolutionEvaluate the following :
(i) i7
(ii) i51
(iii) 1i
(iv) i−71
(v) (i37+1i67)View SolutionEvaluate : (i37+1i67)
View SolutionSimplify the following :
(i) i97
(ii) i8
(iii) 1i3
(iv) (−i)14
(v) i−22
(vi) i−63View SolutionEvaluate: (i) (i41+1i71) (ii) (i53+1i53)
View Solution