एक समबाहु त्रिभुज का क्षेत्रफल 17300cm2 है। त्रिभुज के प्रत्येक शीर्ष को केन्द्र लेकर एक वृत्त खींचा गया ह। वृत्त की त्रिज्या समबाहु त्रिभुज की भुजा की लंबाई के आधा है । त्रिभुज के उस भाग का क्षेत्रफल ज्ञात कीजिए जो वृत्त में नहीं है। (π=3.14 और √3=1.73)
The correct Answer is:1600cm2
Step by step video, text & image solution for एक समबाहु त्रिभुज का क्षेत्रफल 17300cm^2 है। त्रिभुज के प्रत्येक शीर्ष को केन्द्र लेकर एक वृत्त खींचा गया ह। वृत्त की त्रिज्या समबाहु त्रिभुज की भुजा की लंबाई के आधा है । त्रिभुज के उस भाग का क्षेत्रफल ज्ञात कीजिए जो वृत्त में नहीं है। (pi=3.14 और sqrt3=1.73) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Related Playlists
- BOOK - MBD HINDI-HARYANA BOARDCHAPTER - वृत्तो से सम्बंधित क्षैत्रफलEXERCISE - बहुविकल्पीय प्रशन15videos
वृत्तो से सम्बंधित क्षैत्रफल
- BOOK - MBD HINDI-HARYANA BOARDCHAPTER - वृत्तो से सम्बंधित क्षैत्रफलEXERCISE - प्रशनावली 12.318videos
वृत्तो से सम्बंधित क्षैत्रफल
- BOOK - MBD HINDI-HARYANA BOARDCHAPTER - वृत्तEXERCISE - लघु उत्तरात्मक प्रश्न10videos
वृत्त
- BOOK - MBD HINDI-HARYANA BOARDCHAPTER - वृत्तों से सम्बन्धित क्षेत्रफलEXERCISE - लघु उत्तरात्मक प्रश्न18videos
वृत्तों से सम्बन्धित क्षेत्रफल
Similar Questions
उस वृत्त की त्रिज्या क्या होगी जिसकी परिधि 44 सेमी हो।
07:55View Solution(जब तक अन्यथा न कहा जाए, π=227 का प्रयोग कीजिए।) आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि PQ=24cm, PR=7cm तथा O वृत्त का केंद्र है।
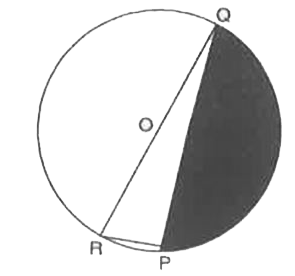 07:05View Solution
07:05View Solutionकीजिए कि दो संकेंद्रीय वृत्तों में बड़े वृत्त की जीवा जो छोटे वृत्त को स्पर्श करती है, स्पर्श बिन्दु पर समद्विभाजित होती है।
02:40View Solutionएक वृत्त की परिधि ज्ञात कीजिए जिसका क्षेत्रफल 6.16सेमी2 है।
05:14View Solutionसिद्ध कीजिये की बिंदु (a,a),(-a,-a),(-a√3,a√3) एक समबाहु त्रिभुज के निर्देशांक है
02:26View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
02:01View Solutionएक त्रिभुज का क्षेत्रफल ज्ञात किजिए जिसके शीर्ष बिंदु A(1,1,1),B(1,2,3) और C(2,3,4) है।
34:41View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
10:06View Solutionएक समबाहु त्रिभुज की भुजाएँ 2 सेमी/से की दर से बढ़ रही है। क्षेत्रफल के बढ़ने की दर, जबकि भुजा 10 सेमी हो, है
02:59View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
02:00View SolutionRevision |दो विशेष त्रिभुज : समबाहु तथा समद्विबाहु #!#एक त्रिभुज की दो भुजाओं की मापों का योग
01:13View SolutionAn equilateral triangle ABC is insribed in a circle as shown figure. A square of largest possible area is made inside this triangle as shown. Another circle made inscribing the square. What is the ratio of area of large circle and the small circle? जैसा की आकृति में दर्शाया गया है, एक समबाहु त्रिभुज ABC एक वृत्त में बनाया गया है। जैसा दर्शाया गया है, सबसे बड़े संभावित क्षेत्रफल वाला वर्ग इस त्रिभुज के अंदर बनाया गया है। बड़े वृत्त तथा छोटे वृत्त के क्षेत्रफल का अनुपात क्या है?
01:09View SolutionPerimeter of an equilateral triangle is equal to the circumference of a circle. The ratio of their areas is (Use pi=22/7 ) एक समभुज त्रिभुज का परिमाप एक वृत्त की परिधि के बराबर है। उनके क्षेत्रफल का अनुपात क्या है? ( pi=22/7 का प्रयोग करें)
01:15View SolutionTwelve sticks, each of length one unit, are used to form an right-angled triangle. The area of the triangle is :
बारह छड़ियाँ, जिनमें से प्रत्येक की लंबाई एक इकाई है, का इस्तेमाल एक समकोण त्रिभुज बनाने के लिए किया जाता है | इस त्रिभुज का क्षेत्रफल ज्ञात करें |01:27View SolutionThe side of an equilateral triangle is 4 cm. What is its area ?
एक समबाहु त्रिभुज की भुजा 4 cm है | उसका क्षेत्रफल कितना है?00:52View SolutionIf the radius of the circumcircle of an equilateral triangle is 8 cm, then the measure of radius of its incircle is: यदि एक समबाहु त्रिभुज के परिवृत्त की त्रिज्या 8 सेमी है, तो इसके अंतः वृत्त की त्रिज्या का मान ज्ञात करें |
43:44View Solution


