Draw the graph of y=(x−1)(6x−1)2x−1.
Video Solution
Text Solution
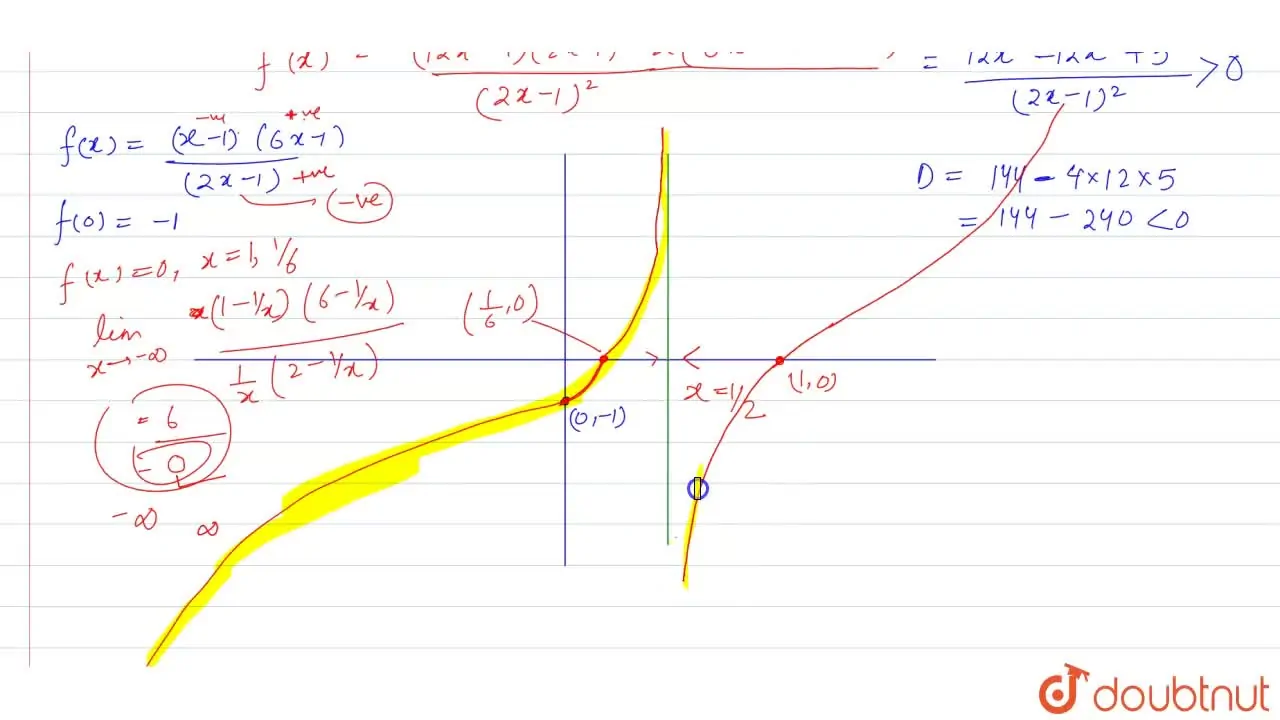
We have y=f(x)=(x−1)(6x−1)2x−1.
The domain of the function is R−{1/2}.
1. y-intercept f(0)=1 So the graph cuts the y-axis at (0,-1).
2. x-intercept (zeros)
Put y=0 or (x−1)(6x−1)=0
So the graph meets the x-axis at (1/6,0) and (1,0).
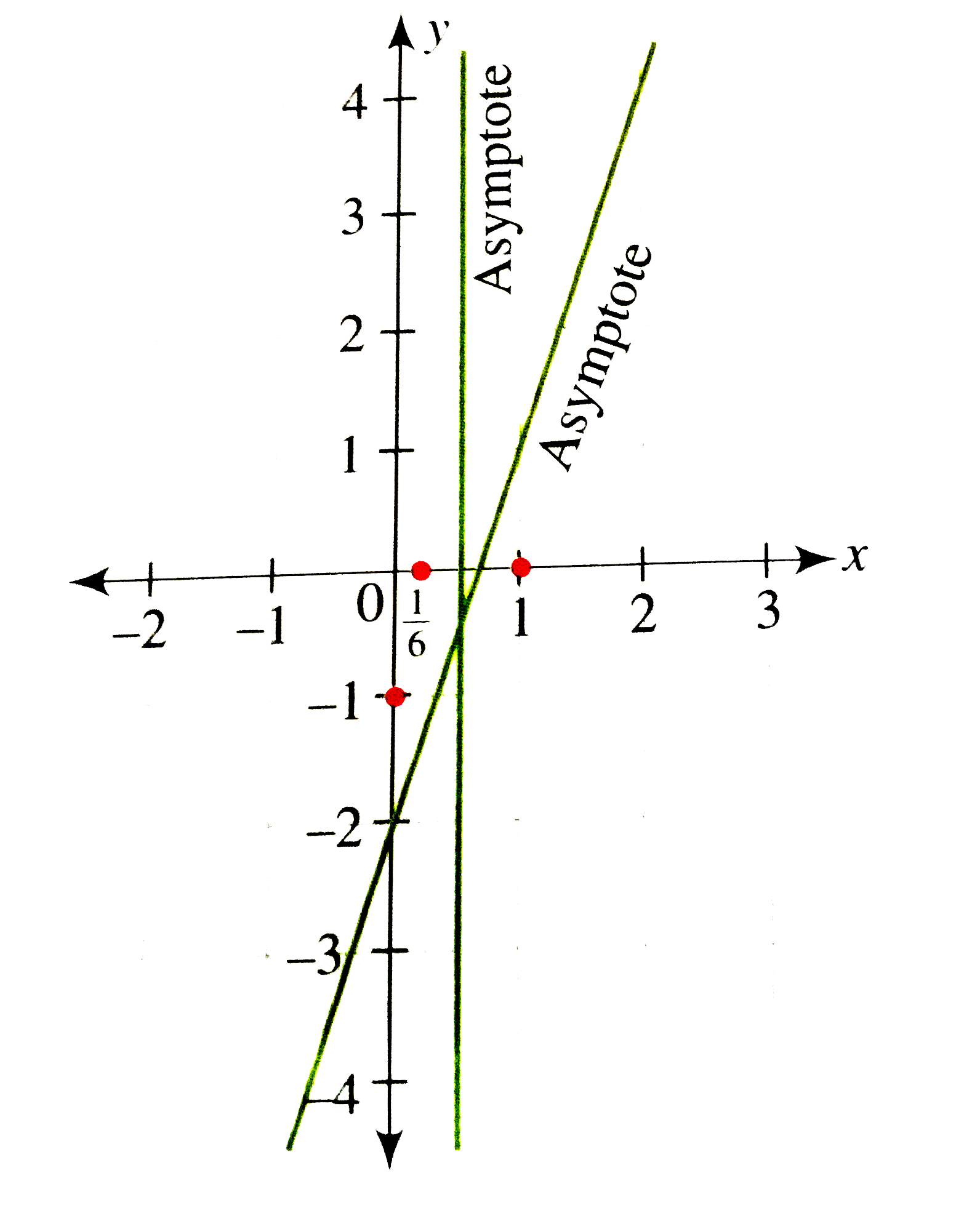
3. Asymptotes
Vertical asymptotes
Clearly, the graph has vertical asymptote x = 1/2, where the denominator becomes zero.
Horizontal asymptotes Clearly, the graph has no horizontal asymptote.
Oblique asymptotes
y=6x2−7x+12x−1
=3x−2−12x−1
Thus, important points and lines are as follows.
4. Momotonicity/Extremum
f'(x)=(12x−7)(2x−1)−2(6x2−7x+1)(2x−1)2
=(12x2−12x+5)(2x−1)2>0,∀x∈R−{1/2}
Hence the function is increasing throughout.
limx→−∞(x−1)(6x−1)2x−1=−∞ and limx→1−2(x−1)(6x−1)2x−1=∞
Thus, f(x) increases from −∞ to ∞ when x increases from −∞ to 1/2 crossing the x-axis at (1/6,0) and approaching asymptote y=3x−2 to the left of it.
limx→1+2(x−1)(6x−1)2x−1=−∞ and limx→∞(x−1)(6x−1)2x−1=∞
Thus, f(x) increases from −∞ to ∞ when x increases from 1/2 to ∞ crossing the x-axis at (1,0) . f(x) approaches asymptote y=3x−2 to the right of the asymptote.
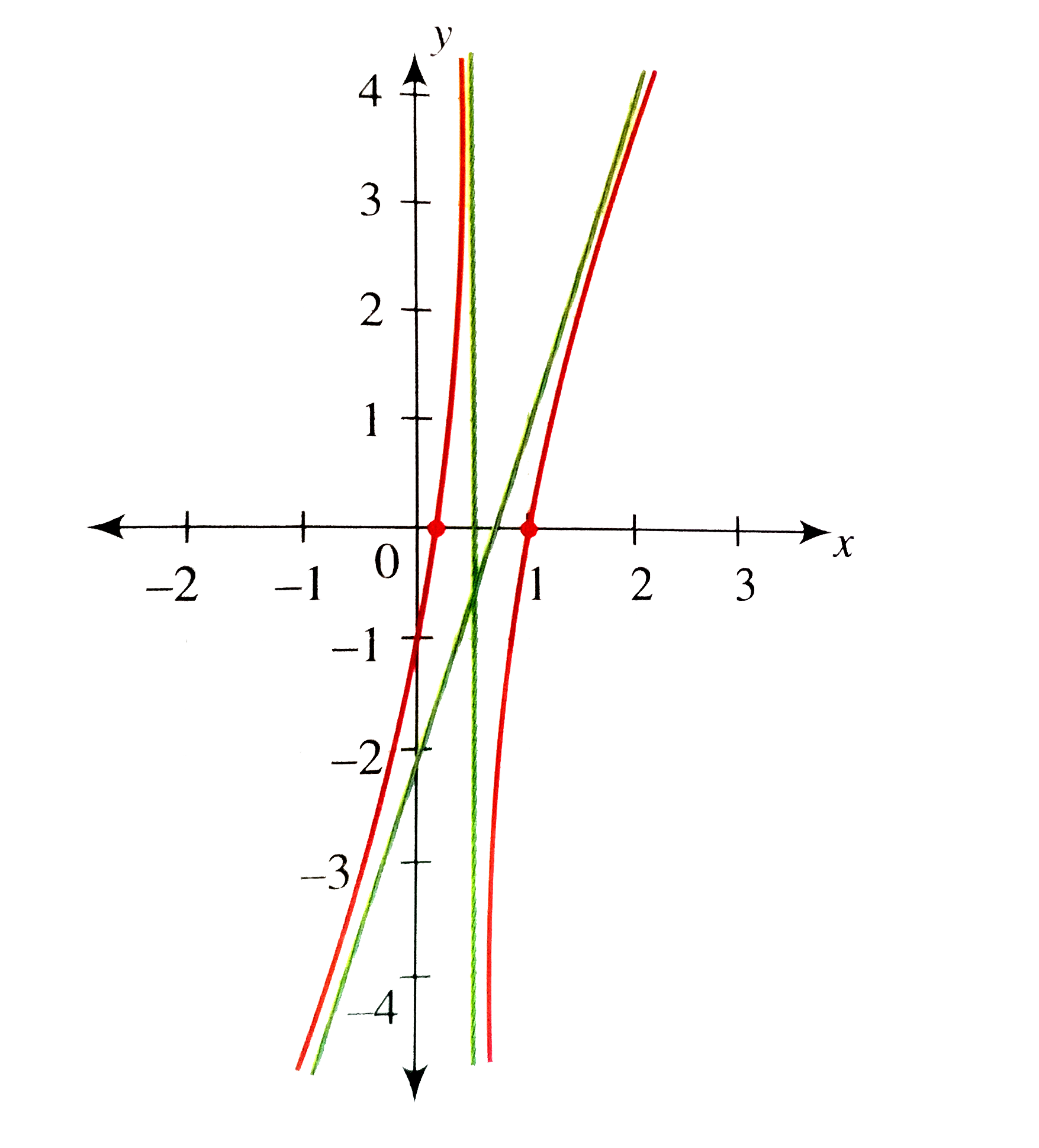
Hence the graph of y=f(x) can be drawn as shown in the following figure.
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises17videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - ILLUSTRATION78videos
GRAPHICAL TRANSFORMATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES34videos
GRAPHS OF ELEMENTARY FUNCTIONS
Similar Questions
Draw the graph of y=2x−1
View SolutionDraw the graph of y=x−1x−2.
View SolutionDraw the graph of y=√xx−1
View SolutionDraw the graph of y=x+1x
View SolutionDraw the graph for |y|=(x−1)(x−2).
View SolutionDraw the graph of |y|=(x−1)(x−2)(x−3).
View SolutionDraw the graph of y=sin−1,1x
View SolutionDraw the graph of y=√x−11+x
View SolutionDraw the graph of y=sin−1(x2)
View SolutionDraw the graph of y=sin−1(x−3).
View Solution