Question

Draw the graph of the rational function $f\left(x\right)=\frac{x^2-1}{x-1}$

Explanation

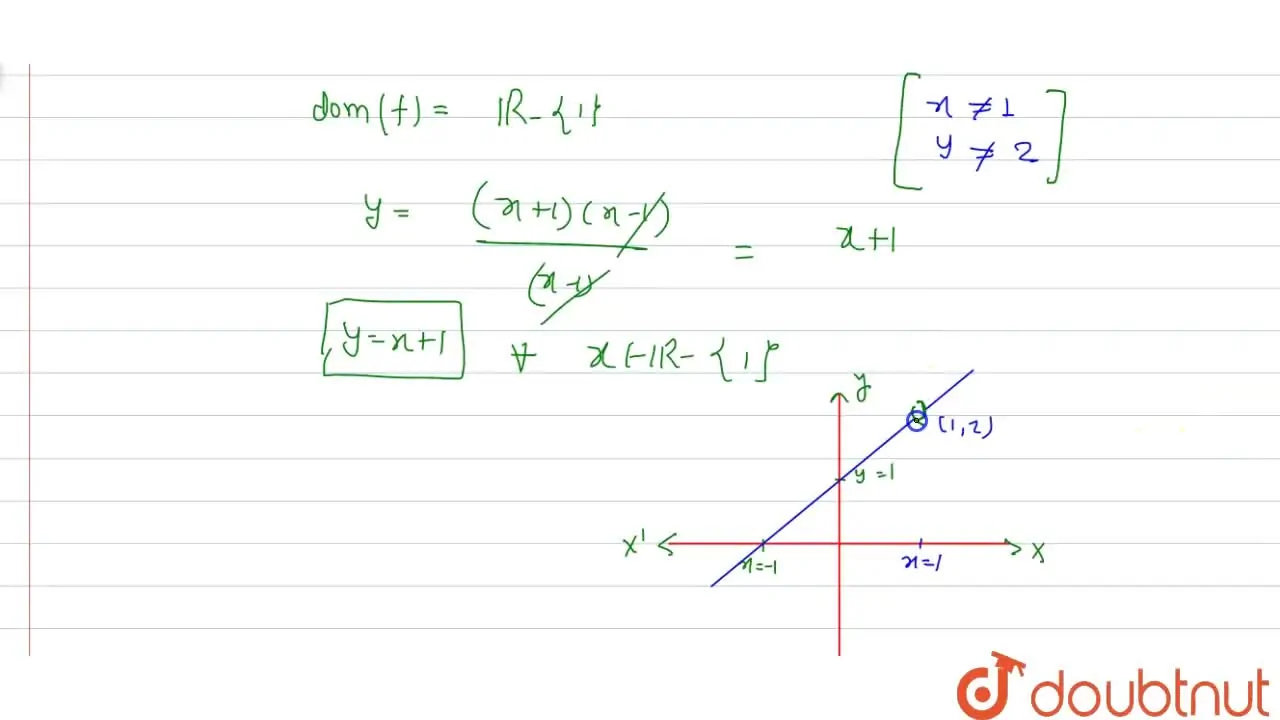
Let ` f(x) = (x^(2) -1)/(x-1) `
Now, ` f(1)= 0/0` , which is meaningless.
So, the funcation it not defined at x=1.
Also, when ` x ne 1`, we have
` f (x) = (( x^(2)-1)/(x-1))= (x +1)`
The being a linear funcation, its graph is a straight line.
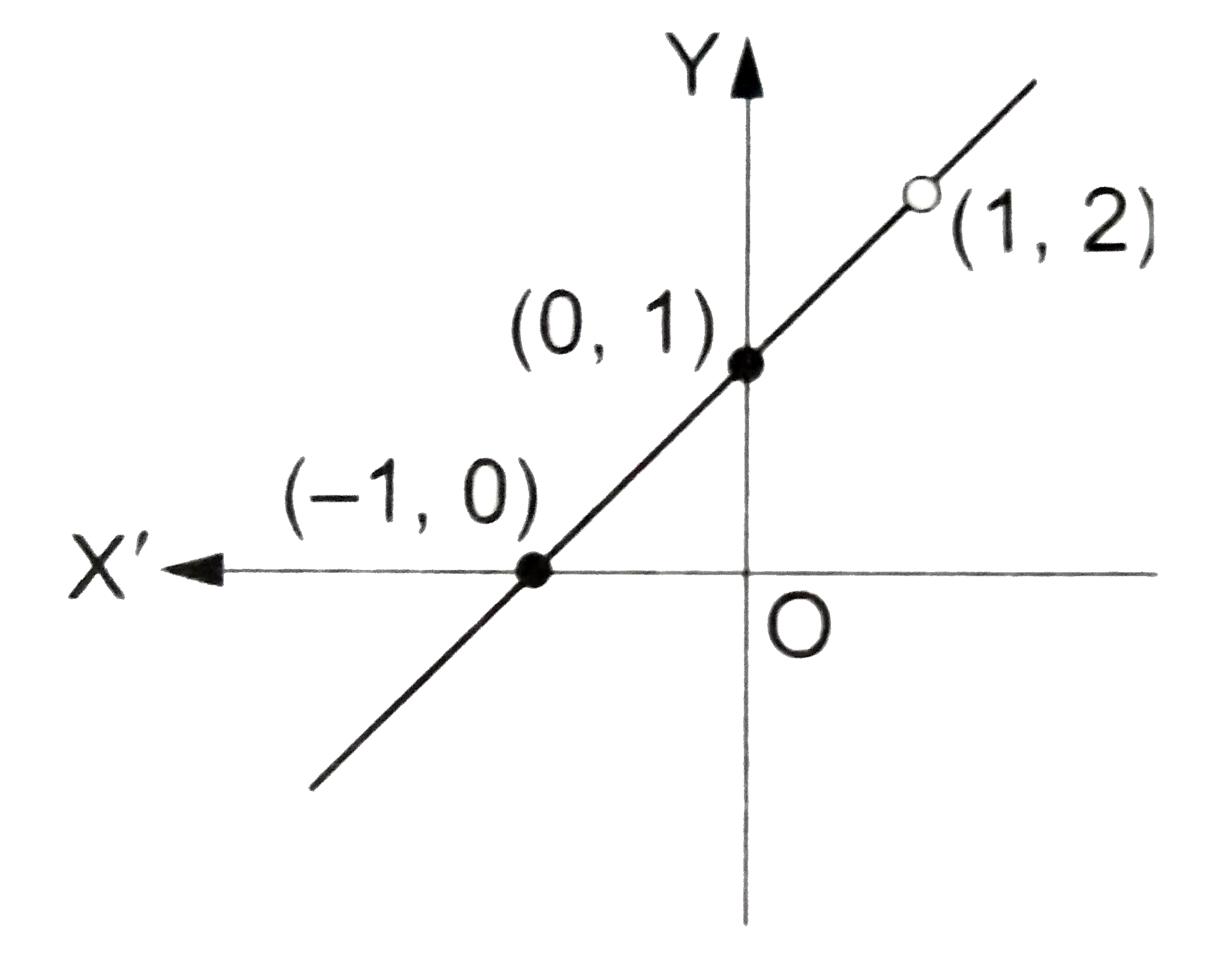
Some, of the points on the graph are (0,1) , (-1,0) , (2,3) ,(3,4) (-2, -=1) , (-3,-2) etc.
Joining these points, we obtain the required graph. Clearly, the point (1,2) does not lie on the graph. so, it is a broken graph , and we shall say that given function is discontinuous at x= 1.