Draw the graph of the function .
Video Solution
Text Solution
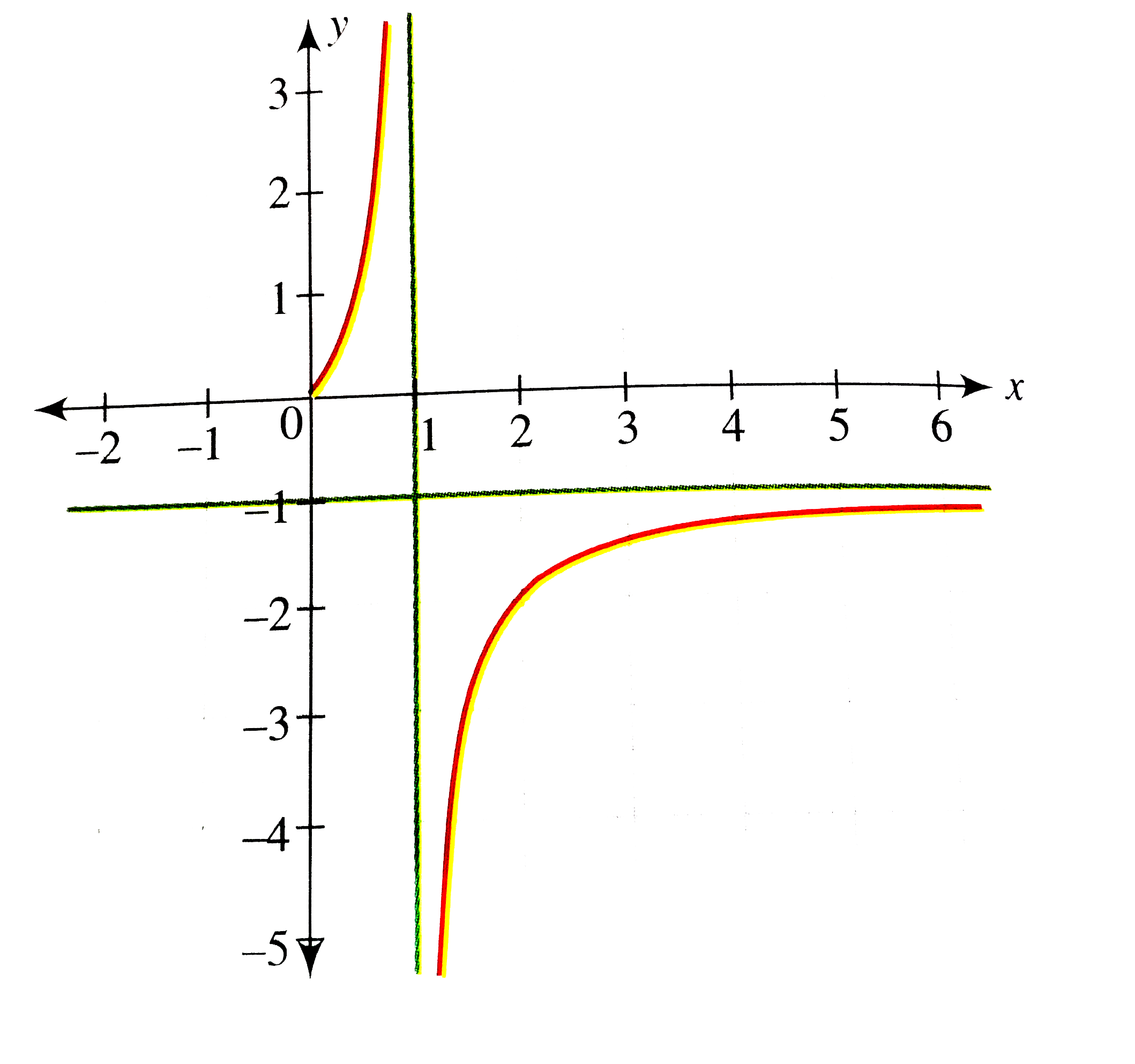
So , which is a rectangular hyperbola having centre at (1,-1).
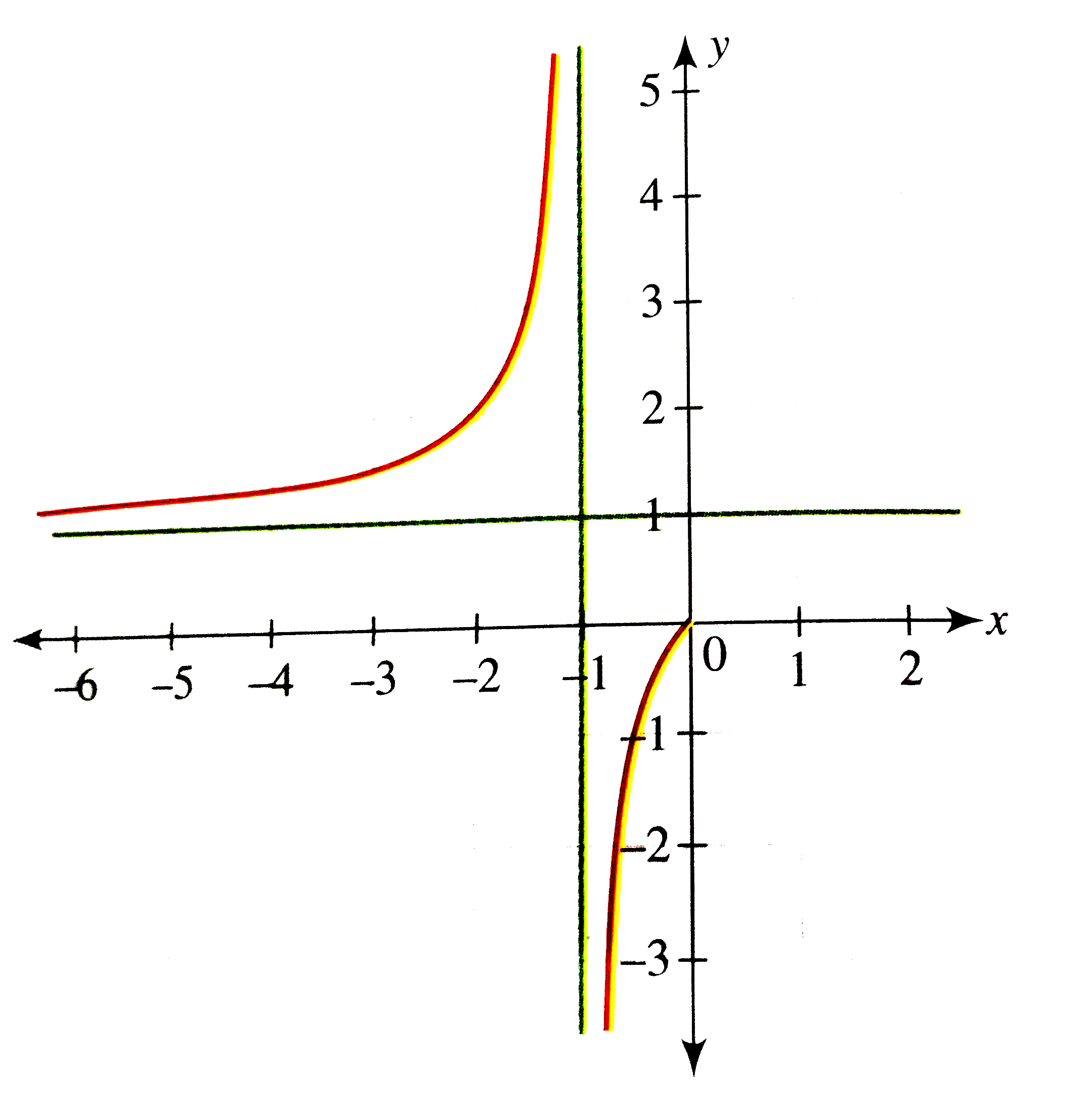
So , which is a rectangular having centre at (-1,1).
The graph is as shown in the following figure.
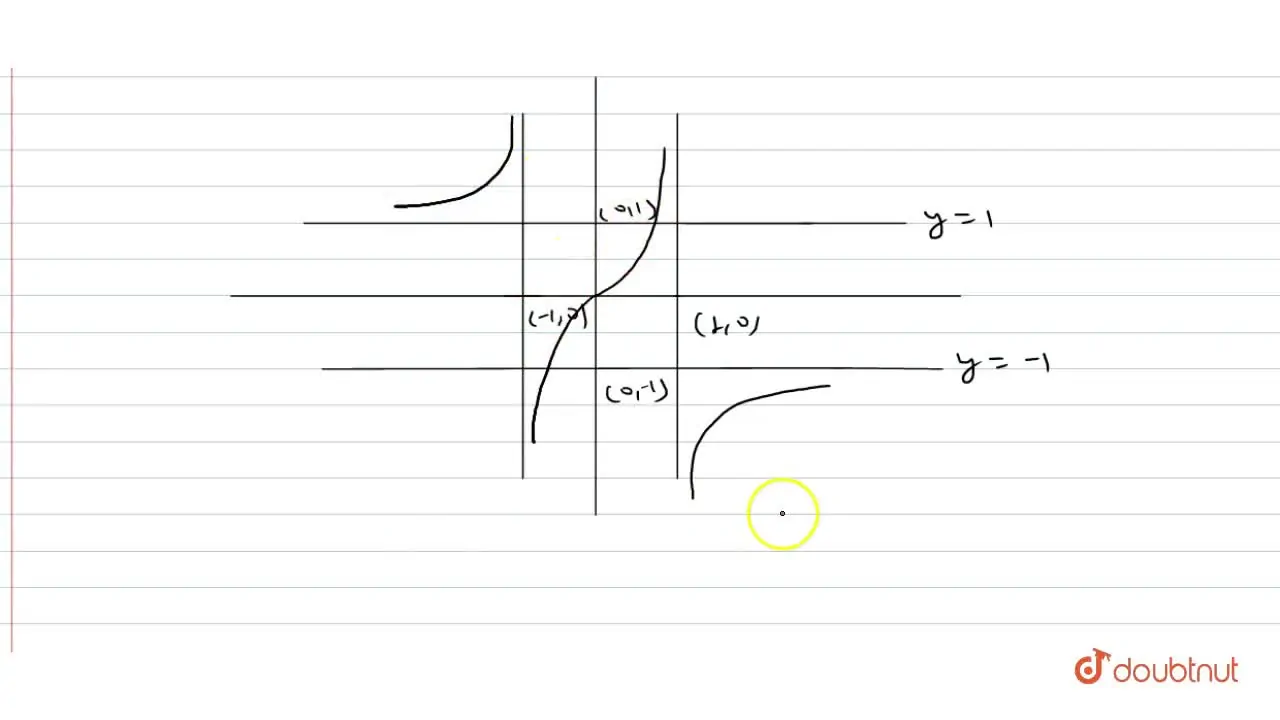
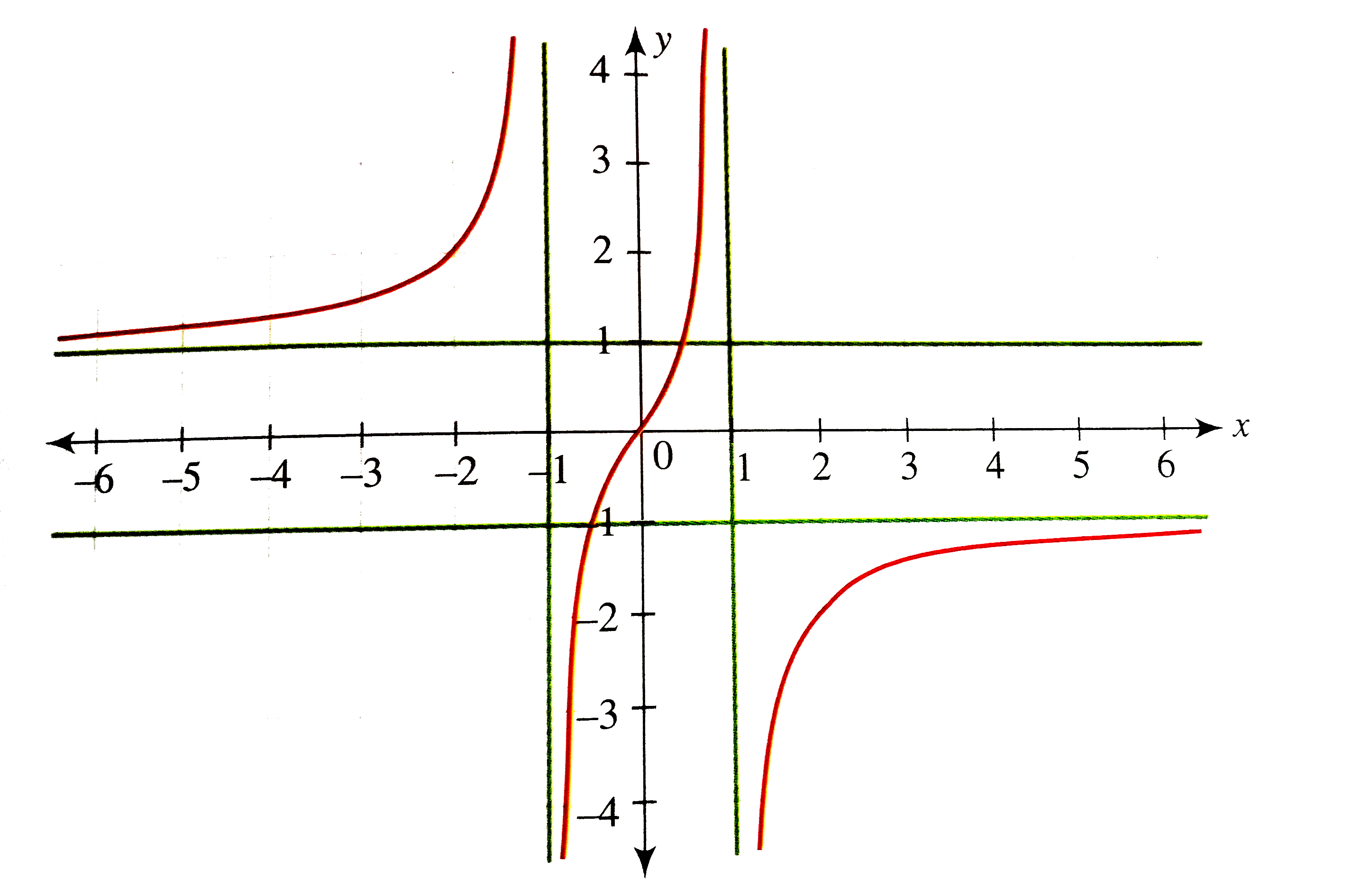
Combining two cases, we get the following graph.
Alternative method
The function has vertical asymptotes as .
Also the function has horizontal asymptotes.
For
For
Graph intersect axis at (0,0)
Hence is an increasing function.
From the above discussion, we have the following reference points and lines.
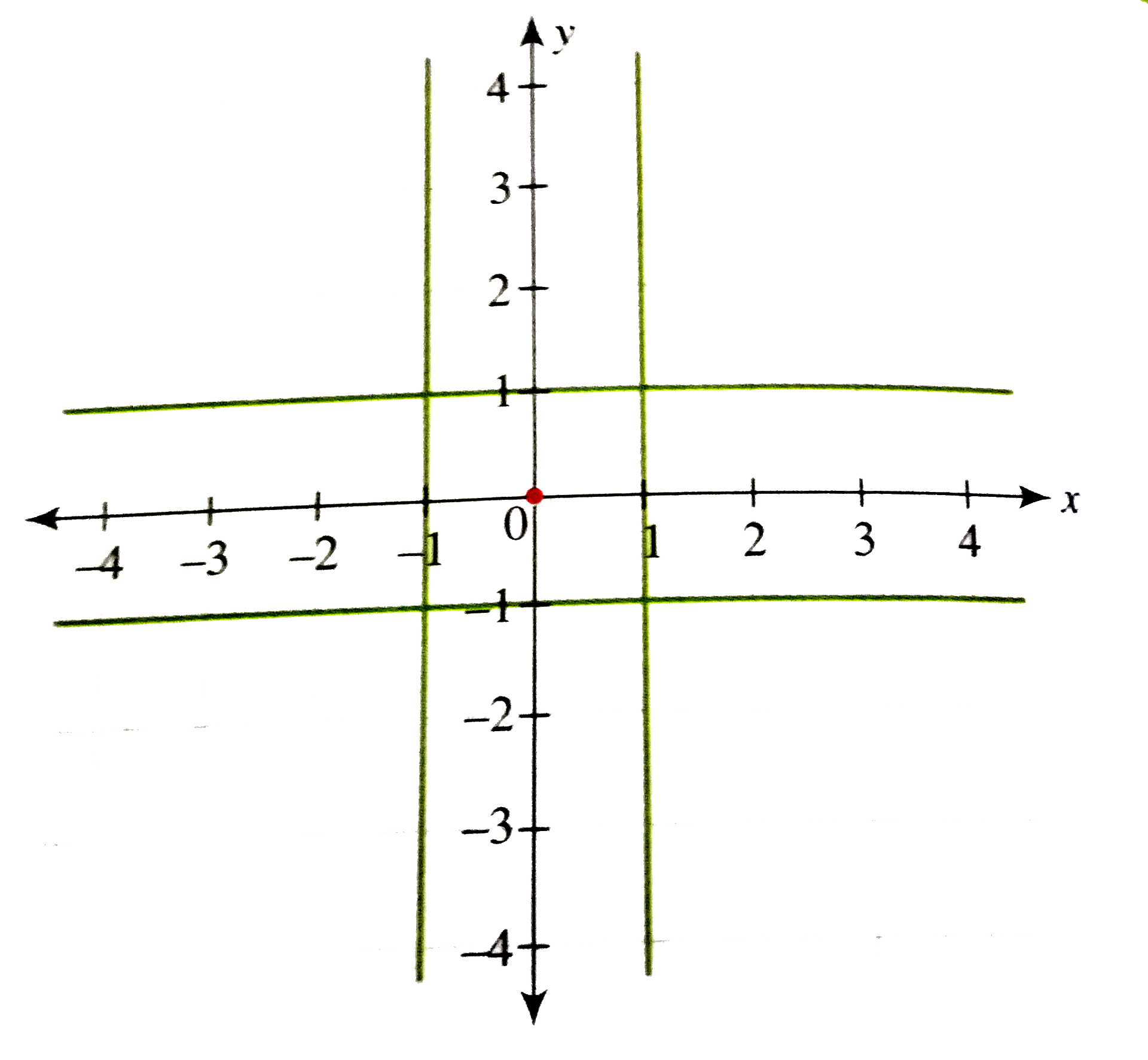
In the above figure, we have three regions, .
In each region, in increasing.
and
and
Hence the graph for is as shown in the following figure.
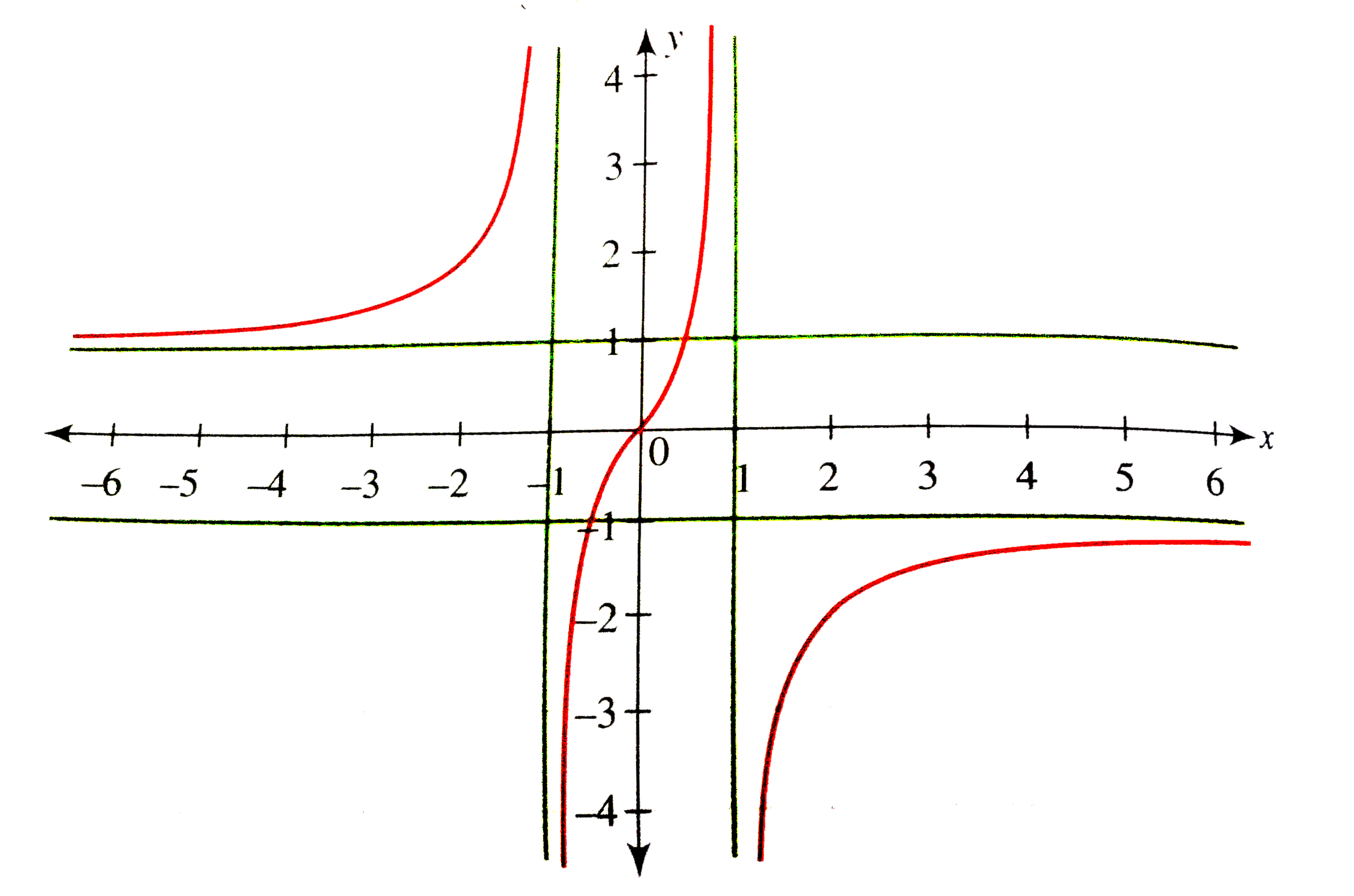
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise13videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise22videos
GRAPHICAL TRANSFORMATIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
Similar Questions
Draw the graph of the function f(x)=|x|+|x−1|
View SolutionDraw the graph of the function f(x)=(1x)x
View SolutionDraw the graph of the function f(x)=(1+1x)2
View SolutionDraw the graph of the function: f:R→R defined by f(x)=x3,x∈R
View SolutionDraw the graph of the function: f(x)=−|x−1|12
View SolutionDraw the graph of the function f:R→Rdefined by f(x)=x3, x∈R.
View SolutionThe graph of the function f:R→R defined by f(x)=|x|2+|x|1+x2 may lie in :
View SolutionThe function f:R→R is defined by f(x)=(x−1)(x−2)(x−3) is
View SolutionThe function f:R→R defined by f(x)=(x−1)(x−2)(x−3) is
View SolutionConsider function f:R−{−1,1}→R. f(x)=x1−|x| Then the incorrect statement is
View Solution