Draw the graph of f(x)=2x+3x2/3 and discuss the type of non-differentiability for the function. Also find the point of inflection.
Video Solution
Text Solution
We have f(x)=2x+3x2/3
∴f′(x)=2+3.23x−13=2(1+x−1/3)
∴f′(x)=2+3.23x−1/3=2(1+x−1/3) ltbr Let f′(x)=0
⇒x1/3+1=0⇒x=−1
⇒f''(x)=−23x−1
and f''(−1)=−23(−1)4/3=−23<0
So x=−1 is the point of maxima.
Also, f′(0) does not exist due to the vertical tangent.
Hence f(x) is non-differentiable at x=0
The graph of the function is as shown in the following figure.
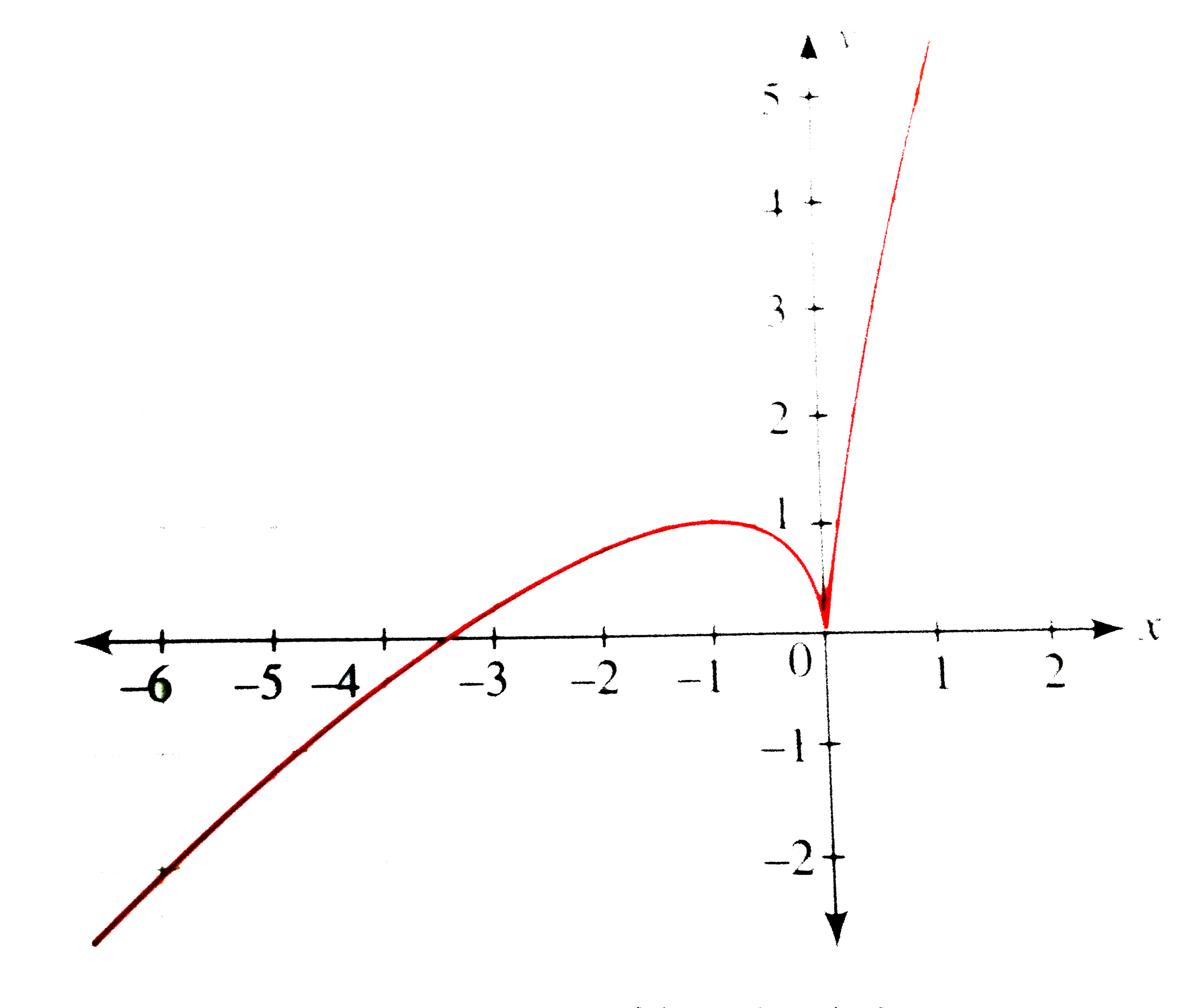
From the graph, x=0 is the point of local minima.
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Draw the graph of f(x)=x2−3
View SolutionDraw the graph of f(x)=x3−xx2−1.
View SolutionDraw the graph of:
y=f(x)=3sin(2x−1).View SolutionDraw the graph of f(x)=(x−1)|(x−2)(x−3)|.
View SolutionDraw the graph of y=xex. Find the range of the function. Also find the point of inflection.
View SolutionDraw the graph of f(x)=5x2(x−1)3.
View SolutionDiscuss the differentiability of function f(x)=x−∣∣x−x2∣∣
View SolutionDraw the graph of f(x)=e−x2. Discuss the concavity of the graph.
View SolutionDraw the graph of the function f(x)=x−∣∣x−x2∣∣,−1≤x≤1 and find the points of non-differentiability.
View SolutionDraw the graph of f(x)=|x|−|2x−3|. Find the range of the function.
View Solution