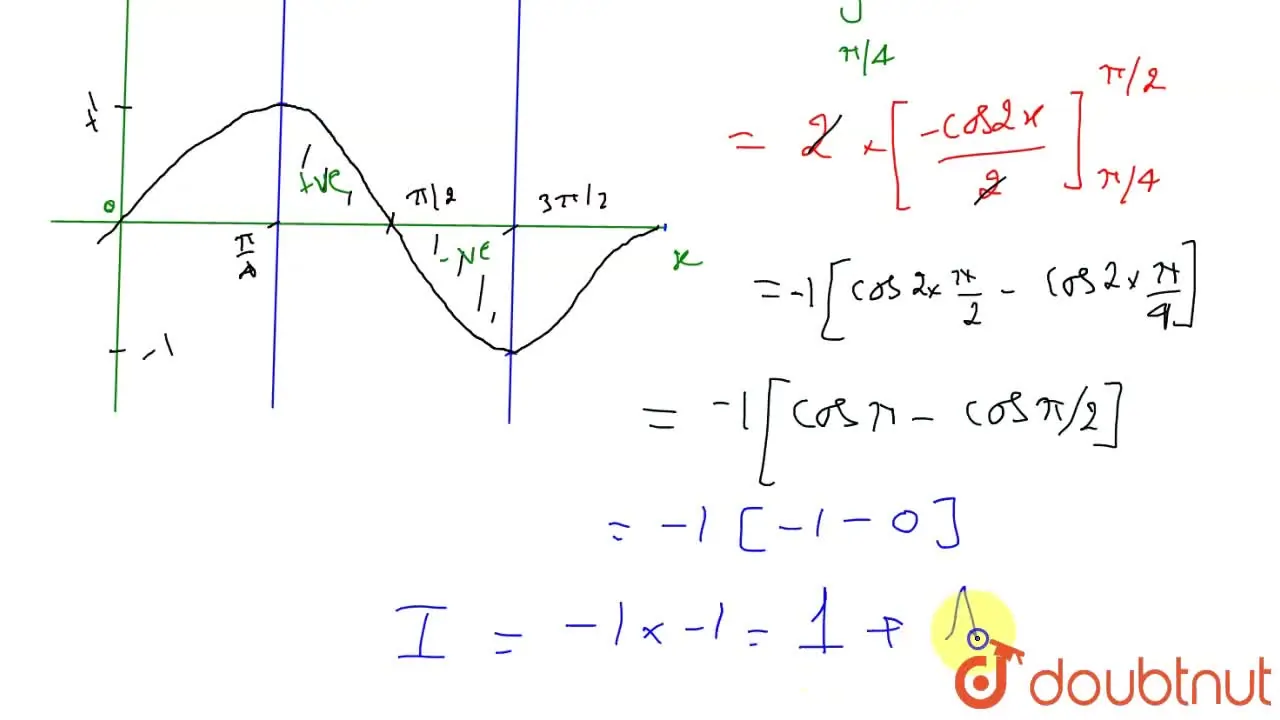
Draw a rough sketch of y=sin2x and determine the area enclosed by the curve. X-axis and the lines x=π/4 and x=3π/4.
The correct Answer is:1 sq unit
Step by step video & image solution for Draw a rough sketch of y=sin 2x and determine the area enclosed by the curve. X-axis and the lines x=pi//4 and x=3pi//4. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - AREA OF BOUNDED REGIONSEXERCISE - Exercise For Session 219videos
AREA OF BOUNDED REGIONS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - AREA OF BOUNDED REGIONSEXERCISE - Exercise (Single Option Correct Type Questions)24videos
AREA OF BOUNDED REGIONS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - AREA OF BOUNDED REGIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)23videos
AREA OF BOUNDED REGIONS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)21videos
BIONOMIAL THEOREM
Similar Questions
Draw the rough sketch of y2+1=x, x≤2. Find the area enclosed by the curve and the line x=2.
View SolutionDraw a rough sketch of the curve x2+y=9 and find the area enclosed by the curve, the x-axis and the lines x + 1 = 0 and x-2 = 0.
View SolutionDraw a rough sketch of the curve y2=4x and find the area of the region enclosed by the curve and the line y=x.
View SolutionThe area bound by the curve y=secx, then x-axis and the lines x=0andx=π/4, is
View SolutionThe area enclosed by the curve y2+x4=x2 is
View SolutionFind the area enclosed the curve y=sin x and the X-axis between x=0andx=π.
View SolutionFind the area enclosed the curve y=sin x and the X-axis between x=0andx=π.
View SolutionMake a rough sketch of the graph of the function y=4−x2, 0≤x≤2 and determine the area enclosed by the curve, the x-axis and the lines x=0 and x=2.
View SolutionDraw the rough sketch of y= log x. Using integration find the area bounded by the curve, x-axis and x=2
View SolutionDraw a rough sketch of the curve and find the area of the region bounded by curve y2=8x and the line x=2.
View Solution