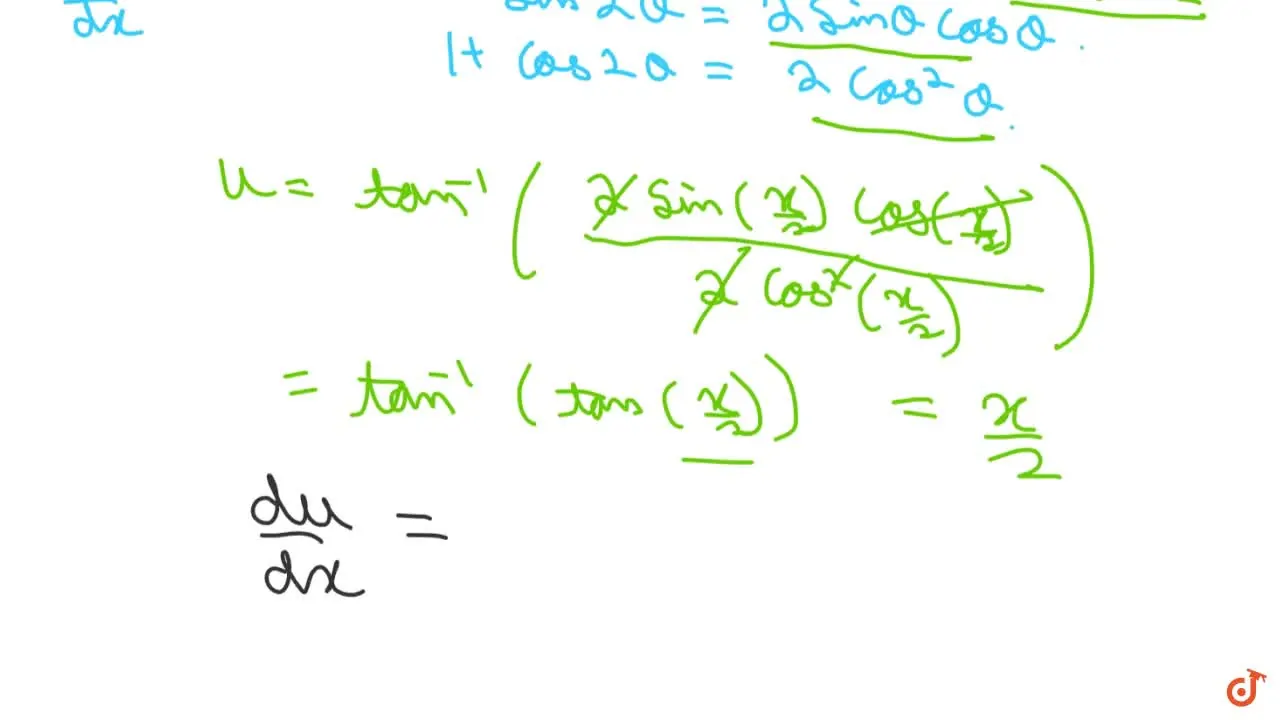Differentiate tan−1(sinx1+cosx), −π<x<π with respect to x
Video Solution
Text Solution
Solution:
We use the chain rule to differentiate the expression but it becomes a lot easier to differentiate this expression when we use trigonometric identities.
As given:
tan−1(1+cosxsinx)
We know the following identities:
cosx=1−tan2(x2)1+tan2(x2) and
sinx=2tan(x2)1+tan2(x2)
Substituting these identities for the expression inside the parentheses in the given expression, we get:
1+cos{x}sin{x}=1+1−tan2(x2)1+tan2(x2)2tan(x2)1+tan2(x2)=22tan(x2)=cot({x}2)=tan(π2−{x}2)
So the given expression now becomes:
tan−1(1+cosxsinx)=tan−1(tan(π2−x2))=π2−x2
So, differentiating the given expression with respect to \{x}, we get:
ddx(tan−1(1+cosxsinx))=ddx(π2−x2)=−12
|
Updated on:21/07/2023
Related Playlists
- BOOK - RD SHARMACHAPTER - DIFFERENTIALS, ERRORS AND APPROXIMATIONSEXERCISE - Solved Examples And Exercises102videos
DIFFERENTIALS, ERRORS AND APPROXIMATIONS
- BOOK - RD SHARMACHAPTER - DIRECTION COSINES AND DIRECTION RATIOSEXERCISE - Solved Examples And Exercises67videos
DIRECTION COSINES AND DIRECTION RATIOS
Similar Questions
Differentiate tan−1(acosx−bsinxbcosx+asinx)w.r.t. x.
View SolutionDifferentiate tan−1{√1−cosx1+cosx}, −π<x<π with respect to x :
View SolutionDifferentiate tan−1{√1+sinx1−sinx},−π2<x<π2 with respect to x :
View SolutionDifferentiate tan−1(11−x+x2)
View SolutionDifferentiate tan−1(4√x1−4x)
View SolutionDifferentiate: tan−1(cosx1+sinx)
View SolutionDifferentiate tan−1(a+x1−ax) with respect to x
View SolutionDifferentiate tan−1(1+cosxsinx) with respect to x.
View SolutionDifferentiate tan−1{cosx+sinxcosx−sinx}, −π4<x<π4 with respect to x
View SolutionDifferentiate tan−1(√1+x2−1x) w.r.t. tan−1x.
View Solution