Differentiate (i) ${sin x}^{3}$ , (ii) ${sin}^{3} x$ , (iii) $e^{sin x}$

Video Solution

Text Solution

Verified by Experts

(i) Let $y = {sin x}^{3}$ .
Put $x^{3} = t$ , so that $y = sin t$ and $t = x^{3}$
$∴ \frac{d y}{d t} = cos t$ and $\frac{d t}{d x} = 3 x^{2}$ .
So, $\frac{d y}{d x} = (\frac{d y}{d t} \times \frac{d t}{d x})$
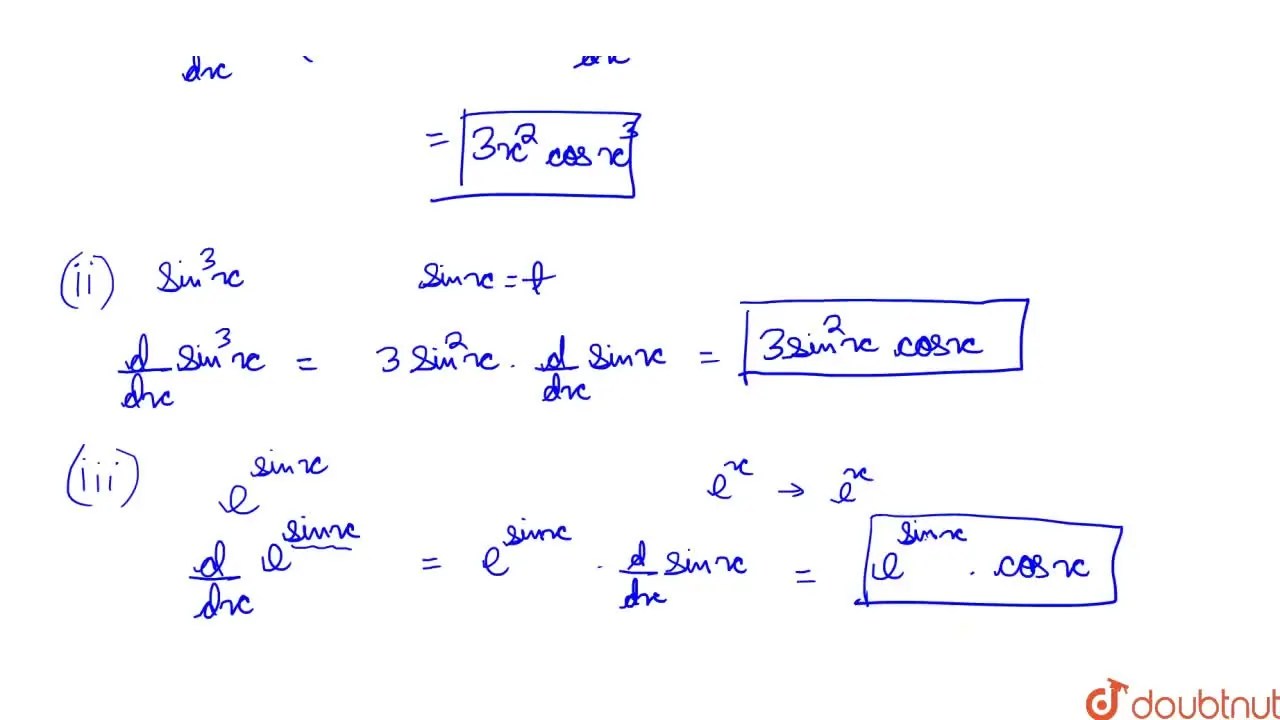
$= 3 x^{2} cos t = 3 x^{2} {cos x}^{3}$ , $[∵ t = x^{3}]$ .
Hence, $\frac{d}{d x} ({sin x}^{3}) = 3 x^{2} {cos x}^{3}$ .
(ii) Let $y = {sin}^{3} x = {(sin x)}^{3}$ .
Put $sin x = t$ , so that $y = t^{3}$ and $t = sin x$ .
$∴ \frac{d}{d t} = 3 t^{2}$ and $\frac{d t}{d x} = cos x$ .
Hence, $\frac{d y}{d x} = (\frac{d y}{d t} \times \frac{d t}{d x})$
$= 3 t^{2} cos x = 3 {sin}^{2} x cos x [∵ t = sin x]$ .
(ii) Let $y = e^{sin x}$
Put $sin x = t$ , so that $y = e^{t}$ and $t = sin x$ .
$∴ \frac{d y}{d t} = e^{t}$ and $\frac{d t}{d x} = cos x$ .
Hence, $\frac{d y}{d x} = (\frac{d y}{d t} \times \frac{d t}{d x})$
$= e^{t} cos x = e^{sin x} . cos x [∵ t = sin x]$ .

Updated on:21/07/2023

|

Class 11 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Differentiate y = (sinx)/(cosx)
A $2 {sec}^{2} x$
B $3 {sec}^{2} x$
C $4 {sec}^{2} x$
D ${sec}^{2} x$

RS AGGARWAL-DIFFERENTIATION-Solved Examples

Home
Ask Doubt
Profile