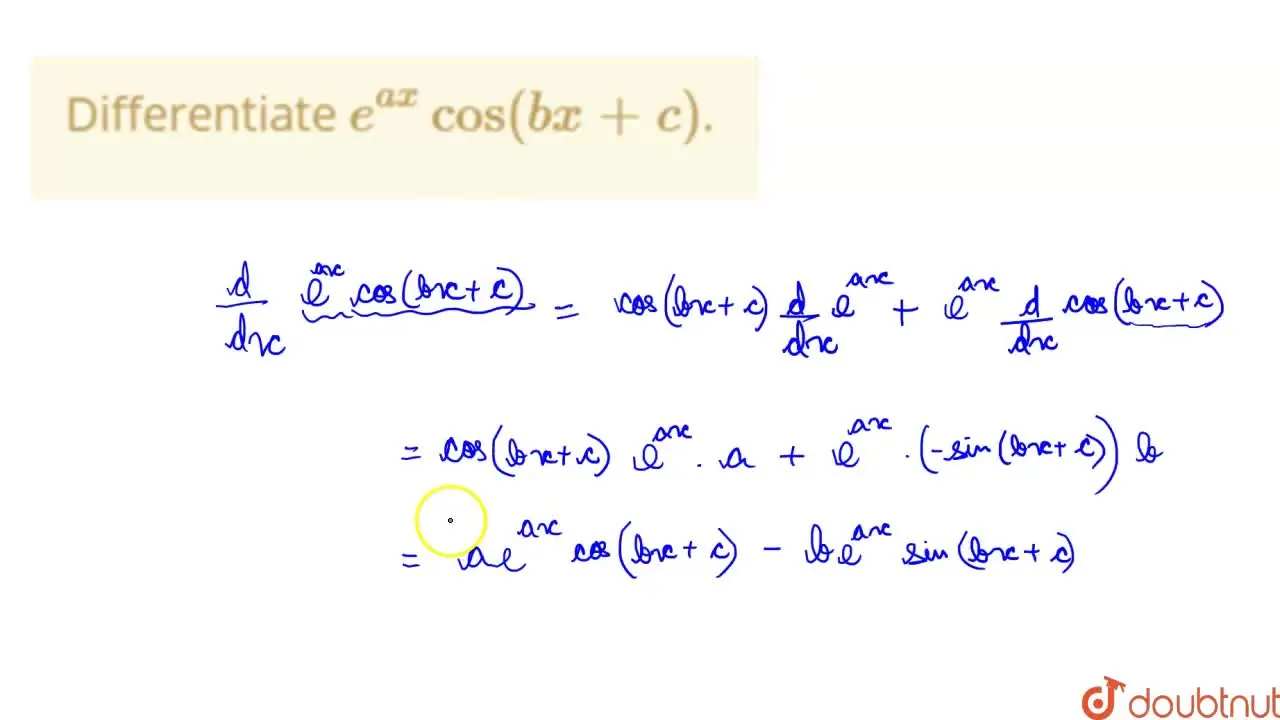Differentiate eaxcos(bx+c).
Video Solution
Text Solution
Using the product rule, we have
ddx[eaxcos(bx+c)]
=eax.ddx[cos(bx+c)]+cos(bx+c).ddx(eax)
=eax[−sin(bx+c)].ddx(bx+c)+cos(bx+c).eax.ddx(ax)
(using the chain rule)
=−beaxsin(bx+c)+aeaxcos(bx+c).
=eax[acos(bx+c)−bsin(bx+c)].
|
Updated on:21/07/2023
Related Playlists
- BOOK - RS AGGARWALCHAPTER - DIFFERENTIATIONEXERCISE - Exrescise 28A13videos
DIFFERENTIATION
- BOOK - RS AGGARWALCHAPTER - DIFFERENTIATIONEXERCISE - Exrescise 28B21videos
DIFFERENTIATION
- BOOK - RS AGGARWALCHAPTER - DIFFERENTIATIONEXERCISE - Exercise 28E44videos
DIFFERENTIATION
- BOOK - RS AGGARWALCHAPTER - CONDITIONAL IDENTITIES INVOLVING THE ANGLES OF A TRIANGLE EXERCISE - EXERCISE 1612videos
CONDITIONAL IDENTITIES INVOLVING THE ANGLES OF A TRIANGLE
- BOOK - RS AGGARWALCHAPTER - ELLIPSEEXERCISE - EXERCISE26videos
ELLIPSE
Similar Questions
Differentiateetanxcosx
View SolutionDifferentiate xex
View SolutionDifferentiate 2xex
View SolutionDifferentiate etanxsinx
View SolutionDifferentiate etanx.sinx
View SolutionDifferentiate −ecosxsinx
View SolutionDifferentiate e3xcos2x with respect to x :
View SolutionDifferentiate (exsinx+xpcosx)
View SolutionDifferentiate e√cotx
View SolutionFind the differentiation of eaxcos(bx+c) w.r.t. x
View Solution