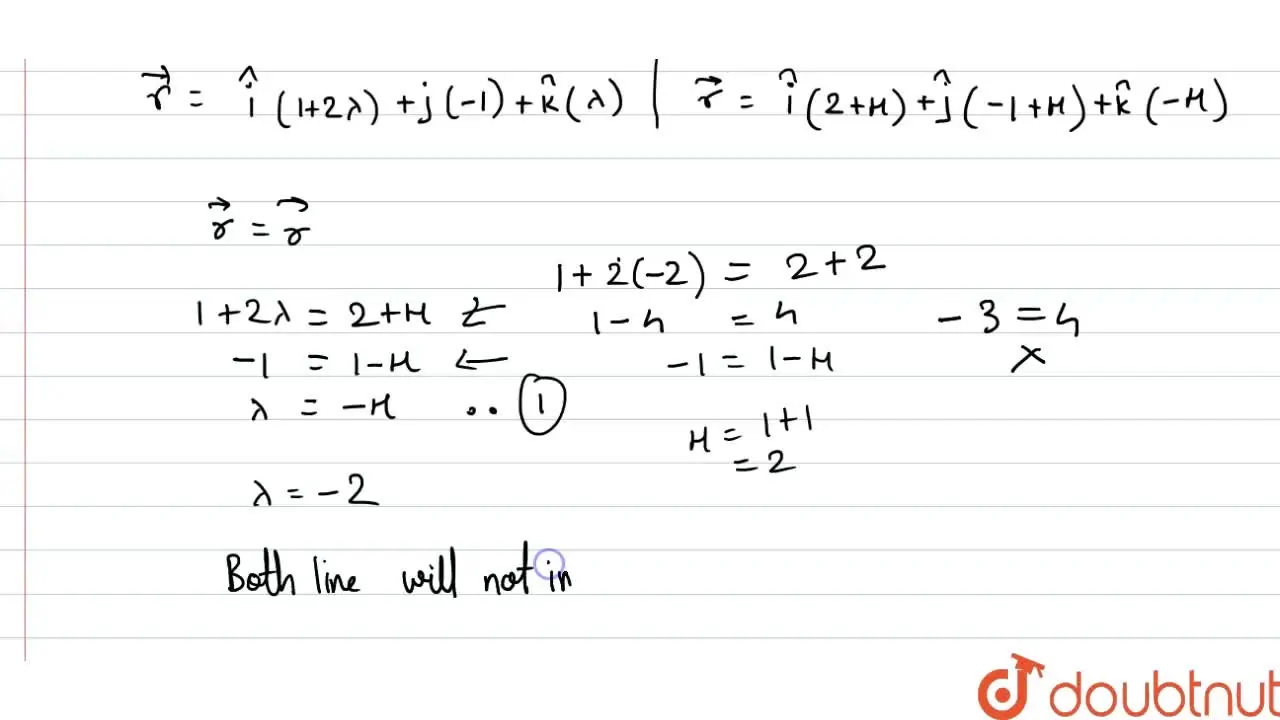Determine whether the following pair of lines intersect or not. i. →r=ˆi−ˆj+λ(2ˆi+ˆk),→r=2ˆi−ˆj+μ(ˆi+ˆj−ˆk)
Here →a1=→i−→j,→a2=2ˆi−ˆj,→b1=2ˆi+ˆkand→b2=ˆi+ˆj−ˆk
Now [→a2−→a1→b1→b2]=∣∣
∣∣2−1−1+1020111−1∣∣
∣∣
=∣∣
∣∣10020111−1∣∣
∣∣
=−1≠0
Thus, the two given lines do not intersect.
ii. Here →a1=ˆi+ˆj−ˆk,→a2=4ˆi−ˆk,→b1=3ˆi−ˆjand→b2=2ˆi+3ˆk
⇒ [→a2−→a1→b1→b2]=∣∣
∣∣4−10−1−1+13−10203∣∣
∣∣
=∣∣
∣∣3−103−10203∣∣
∣∣=0
Thus, the two given lines intersect. Let us obtain the point of intersection of the two given lines.
For some values of λ and μ, the two values of →r must coincide. Thus,
ˆi+ˆj−ˆk+λ(3ˆi−ˆj)=4ˆi−ˆk+μ(2ˆi+3ˆk)
or (3+2μ−3λ)ˆi+(λ−1)ˆj+3μˆk=0
or 3+2μ−3λ=0,λ−1=0,3μ=0
Solving, we obtain λ=1andμ=0
Therefore, the point of intersection is →r=4ˆi−ˆk( by putting μ=0 in the second equation).
Related Playlists
- BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise 3.112videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise 3.215videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank20videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGECHAPTER - TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSEXERCISE - Question Bank34videos
TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONS
Similar Questions
Determine whether the following pair of lines intersect: →r=ˆi−ˆj+λ(2ˆi+ˆk)and→r=2ˆi−ˆj+μ(ˆi+ˆj−ˆk)
View SolutionThe lines →r=(ˆi+ˆj)+λ(ˆi+ˆk)and→r=(ˆi+ˆj)+μ(−ˆi+ˆj−ˆk) are
View SolutionThe lines given by →r=(ˆi−ˆj)+λ(2ˆi+ˆk) and →r=(2ˆi−ˆj)+μ(ˆi+ˆj−ˆk) are
View SolutionFind the shortest distance between the following pair of line: →r=ˆi+ˆj+λ(2ˆi−ˆj+2ˆk),→r=2ˆi+ˆj−ˆk+μ(3ˆi−5ˆj+2ˆk)
View SolutionFind the shortest distance between the following pair of line: →r=ˆi+2ˆj+ˆk+λ(ˆi−ˆj+ˆk)and→r=2ˆi−ˆj−ˆk+μ(2ˆi+ˆj+2ˆk)
View SolutionFind the angle between the following pair of line: →r=3ˆi+ˆj−2ˆk+λ(ˆi−ˆj−2ˆk)and→r=2ˆi−ˆj−56ˆk+μ(3ˆi−5ˆj−3ˆk)
View SolutionFind the angle between each of the following pair of line: →r=5ˆi−7ˆj+λ(−ˆi+4ˆj+2ˆk)→r=−2ˆi+ˆk+μ(3ˆi+3ˆk)
View SolutionFind the shortest distance between the following pair of line: →r=ˆi+2ˆj−4ˆk+λ(2ˆi+3ˆj+6ˆk)and→r=3ˆi+3ˆj−5ˆk+μ(2ˆi+3ˆj+6ˆk).
View SolutionFind the shortest distance between the following lines :
(i) →r=4ˆi−ˆj+λ(ˆi+2ˆj−3ˆk) and
→r=ˆi−ˆj+2ˆk+μ(2ˆi+4ˆj−5ˆk)
(ii) →r=−ˆi+ˆj−ˆk+λ(ˆi+ˆj−ˆk) and
→r=ˆi−ˆj+2ˆk+μ(−ˆi+2ˆj+ˆk)
(iii) x−1−1=y+21=z−3−2 and
x−11=y+12=z+1−2
(iv) x−12=y−23=z−34 and x−23=y−34=z−55
(v) →r=→i+2ˆj+3ˆk+λ(ˆi−ˆj+ˆk) and
→r=2ˆi−ˆj−ˆk+μ(−ˆi+ˆj−ˆk)View SolutionFind the angle between the following pair of line: r=2ˆi≡5ˆj+ˆk+λ(3ˆi+2ˆj+6ˆk)and→r=7ˆi−6ˆk+μ(ˆi+2ˆj+2ˆk)
View Solution